题目内容
6.在Rt△ABC中,∠C=90°,∠A=30°,∠A、∠B、∠C的对边分别是a、b、c,则下列结论错误的是( )| A. | c=2a | B. | a2+b2=c2 | C. | a:b=1:$\sqrt{3}$ | D. | b2=2a2 |
分析 根据直角三角形的性质得到c=2a,根据勾股定理计算,判断即可.
解答 解:∵∠C=90°,∠A=30°,
∴c=2a,A正确,不符合题意;
由勾股定理得,a2+b2=c2,B正确,不符合题意;
b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$a,即a:b=1:$\sqrt{3}$,C正确,不符合题意;
b2=3a2,D错误,符合题意,
故选:D.
点评 本题考查的是勾股定理、直角三角形的性质,直角三角形的两条直角边长分别是a,b,斜边长为c,那么a2+b2=c2.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
11.下列四个不等式组中,解为-1<x<3的不等式组有可能是( )
| A. | $\left\{{\begin{array}{l}{ax>1}\\{bx>1}\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}{ax<2}\\{bx<2}\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}{ax>3}\\{bx<3}\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}{ax<4}\\{bx>4}\end{array}}\right.$ |
18.如果直角三角形的边长为3,4,a,则a的值是( )
| A. | 5 | B. | 6 | C. | $\sqrt{7}$ | D. | 5或$\sqrt{7}$ |
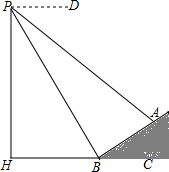 如图,数学学习小组在高600米的山腰(即PH=600米)P处进行测量,测得对面山坡上A处的俯角为30°,山脚B处的俯角α=60°,已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P、H、B、C、A在同一个平面上,点H、B、C在同一条直线上,且PH⊥HC.
如图,数学学习小组在高600米的山腰(即PH=600米)P处进行测量,测得对面山坡上A处的俯角为30°,山脚B处的俯角α=60°,已知tan∠ABC=$\frac{\sqrt{3}}{3}$,点P、H、B、C、A在同一个平面上,点H、B、C在同一条直线上,且PH⊥HC.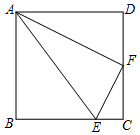 如图,正方形ABCD中,F是CD边的中点,E是BC边上一点,且AF平分∠DAE.
如图,正方形ABCD中,F是CD边的中点,E是BC边上一点,且AF平分∠DAE.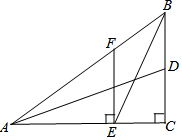 如图△ABC中,∠ACB=90°,AB=10,BC=6,AC=8,BE是∠ABC的角平分线,AD是BC边的中线,EF⊥AC于点E,下列结论正确的有( )个
如图△ABC中,∠ACB=90°,AB=10,BC=6,AC=8,BE是∠ABC的角平分线,AD是BC边的中线,EF⊥AC于点E,下列结论正确的有( )个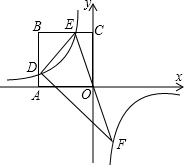 如图,在平面直角坐标系中,x轴上有一点A(a,0),其中a<0,以OA为边长作正方形ABCO,边AB与BC分别交双曲线y=$\frac{k}{x}$第二象限中的一支于点D、E,延长EO交双曲线的另一支于点F,连接DF.
如图,在平面直角坐标系中,x轴上有一点A(a,0),其中a<0,以OA为边长作正方形ABCO,边AB与BC分别交双曲线y=$\frac{k}{x}$第二象限中的一支于点D、E,延长EO交双曲线的另一支于点F,连接DF. “某市道路交通管理条例”规定:小汽车在城市街路上行驶速度不得超过60千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米C处,过了2秒后到达B处,测得小汽车与车速检测仪间距离为50米,请问这辆小汽车超速了吗?为什么?若超速,则超速了多少?
“某市道路交通管理条例”规定:小汽车在城市街路上行驶速度不得超过60千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米C处,过了2秒后到达B处,测得小汽车与车速检测仪间距离为50米,请问这辆小汽车超速了吗?为什么?若超速,则超速了多少?