题目内容
1.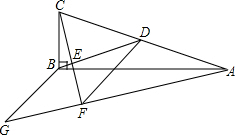 如图,在△ABC中,∠ABC=90°,点D为AC的中点,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
如图,在△ABC中,∠ABC=90°,点D为AC的中点,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(1)证明:四边形BDFG是菱形;
(2)若AC=10,CF=6,求线段AG的长度.
分析 (1)首先可判断四边形BDFG是平行四边形,再由直角三角形斜边中线等于斜边一半,可得BD=FD,则可判断四边形BDFG是菱形;
(2)由菱形的性质求得GF=DF=$\frac{1}{2}$AC=5,由勾股定理得AF的长,继而求得AG的长.
解答 (1)证明:∵AG∥BD,BD=FG,
∴四边形BGFD是平行四边形,
∵CE⊥BD
∴CE⊥AG,
又∵BD为AC的中线,
∴BD=DF=$\frac{1}{2}$AC,
∴四边形BDFG是菱形;
(2)解:∵四边形BDFG是菱形,∠ABC=90°,点D为AC的中点,
∴GF=DF=$\frac{1}{2}$AC=5,
∵CF⊥AG,
∴AF=$\sqrt{{AC}^{2}{-CF}^{2}}$=$\sqrt{{10}^{2}{-6}^{2}}$=8,
∴AG=AF+GF=8+5=13.
点评 本题主要考查了菱形的判定与性质、直角三角形斜边的中线的性质以及勾股定理,注意掌握数形结合思想是解答此题的关键.

练习册系列答案
相关题目
12. 一个不等式组的解集在数轴上的表示如图,则这个不等式组的解集是( )
一个不等式组的解集在数轴上的表示如图,则这个不等式组的解集是( )
 一个不等式组的解集在数轴上的表示如图,则这个不等式组的解集是( )
一个不等式组的解集在数轴上的表示如图,则这个不等式组的解集是( )| A. | -1<x<3 | B. | -1<x≤3 | C. | -1≤x<3 | D. | -1≤x≤3 |
16.下列图形中,既是轴对称图形,又是中心对称图形的是( )
| A. | 直角三角形 | B. | 等边三角形 | C. | 平行四边形 | D. | 矩形 |
13.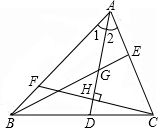 如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上的一点,CF⊥AD于H.下列判断正确的有( )
如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上的一点,CF⊥AD于H.下列判断正确的有( )
 如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上的一点,CF⊥AD于H.下列判断正确的有( )
如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上的一点,CF⊥AD于H.下列判断正确的有( )| A. | AD是△ABE的角平分线 | B. | BE是△ABD边AD上的中线 | ||
| C. | CH为△ACD边AD上的高 | D. | AH为△ABC的角平分线 |
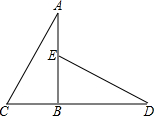 已知:如图,AB⊥CD,垂足为B,点E在AB上,AB=BD,BE=BC,求证:△ABC≌△DBE.
已知:如图,AB⊥CD,垂足为B,点E在AB上,AB=BD,BE=BC,求证:△ABC≌△DBE.