题目内容
13．
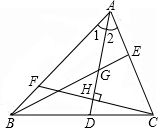如图，在△ABC中，∠1=∠2，G为AD的中点，延长BG交AC于E．F为AB上的一点，CF⊥AD于H．下列判断正确的有（ ）| A． | AD是△ABE的角平分线 | B． | BE是△ABD边AD上的中线 | ||
| C． | CH为△ACD边AD上的高 | D． | AH为△ABC的角平分线 |
分析 根据三角形的角平分线、三角形的中线、三角形的高的概念进行判断．
连接三角形的顶点和对边中点的线段即为三角形的中线；
三角形的一个角的角平分线和对边相交，顶点和交点间的线段叫三角形的角平分线；
从三角形的一个顶点向对边引垂线，顶点和垂足间的线段叫三角形的高．
解答 解：A、根据三角形的角平分线的概念，知AG是△ABE的角平分线，故本选项错误；
B、根据三角形的中线的概念，知BG是△ABD的边AD上的中线，故本选项错误；
C、根据三角形的高的概念，知CH为△ACD的边AD上的高，故本选项正确；
D、根据三角形的角平分线的概念，知AD是△ABC的角平分线，故本选项错误．
故选C．
点评 本题考查了三角形的角平分线、三角形的中线、三角形的高的概念，注意：三角形的角平分线、中线、高都是线段，且都是顶点和三角形的某条边相交的交点之间的线段．透彻理解定义是解题的关键．
练习册系列答案
出彩同步大试卷系列答案
相关题目
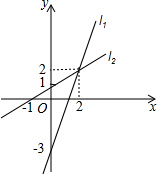已知l1、l2的解析式分别为y1=ax+b，y2=mx+n（a＞m＞0），如图是l1、l2的图象，根据图象回答以下问题：
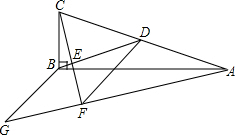如图，在△ABC中，∠ABC=90°，点D为AC的中点，过点C作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．
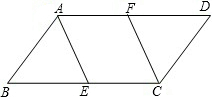已知：如图，在?ABCD中，E、F分别是BC、AD上的点，BE=DF．
18．在平面直角坐标系中，点M（-5，-3m+4）在第三象限，则m的取值范围是（ ）
| A． | m＜$\frac{4}{3}$ | B． | m＞-$\frac{4}{3}$ | C． | m＞$\frac{4}{3}$ | D． | m＜-$\frac{4}{3}$ |
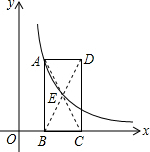已知如图：矩形ABCD的边BC在x轴上，E为对角线AC、BD的交点，点B、D的坐标分别为B（1，0），D（3，3）．