题目内容
9.(1)若P为x轴上一动点,A(2,2),B(4,4),求PA+PB最小值?(2)若P为半径为1的⊙O上一动点,O(0,0),A(2,2),B(4,4),求PA+PB的最小值?
分析 (1)作点A关于x轴的对称点A′,当点A′、P、B在一条直线上时,PA+PB有最小值,利用两点间的距离公式求得A′B的距离即可;
(2)先求得OA、OB的长度,然后根据PA+PB=OA+OB-2OP计算即可.
解答 解:(1)如图1所示;作点A关于x轴的对称点A′.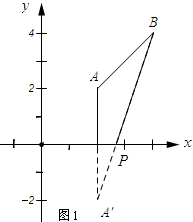
由轴对称的性质可知点A′的坐标为(2,-2),
∵PA+PB=PA′+PB.
当点A′、P、B在一条直线上时,PA+PB有最小值.
由两点间的距离公式得:A′B=$\sqrt{(4-2)^{2}+(4+2)^{2}}$=2$\sqrt{10}$.
∴PA+PB的最小值为2$\sqrt{10}$.
(2)如图2所示:当点A、B、P在一条直线上时,PA+PB有最小值.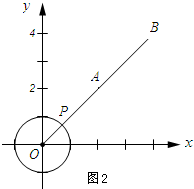
由两点之间的距离公式得:OA=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$,OB=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
AP+PB=OA+OB-2OP=6$\sqrt{2}$-2.
∴PA+PB的最小值为6$\sqrt{2}-2$.
点评 本题主要考查的是轴对称--最短路径问题,明确PA+PB有最小值的条件是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
17.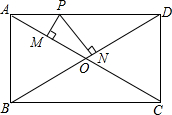 如图,矩形ABCD中,对角线AC与BD相交于点O,P为AD上的动点,过点P作PM⊥AC,PN⊥BD,垂足分别为M、N,若AB=m,BC=n,则PM+PN=( )
如图,矩形ABCD中,对角线AC与BD相交于点O,P为AD上的动点,过点P作PM⊥AC,PN⊥BD,垂足分别为M、N,若AB=m,BC=n,则PM+PN=( )
 如图,矩形ABCD中,对角线AC与BD相交于点O,P为AD上的动点,过点P作PM⊥AC,PN⊥BD,垂足分别为M、N,若AB=m,BC=n,则PM+PN=( )
如图,矩形ABCD中,对角线AC与BD相交于点O,P为AD上的动点,过点P作PM⊥AC,PN⊥BD,垂足分别为M、N,若AB=m,BC=n,则PM+PN=( )| A. | $\frac{m+n}{2}$ | B. | $\frac{mn}{m+n}$ | C. | $\frac{mn}{{\sqrt{m_{\;}^2+{n^2}}}}$ | D. | $\frac{n}{m}$ |
18.在平面直角坐标系中,点M(-5,-3m+4)在第三象限,则m的取值范围是( )
| A. | m<$\frac{4}{3}$ | B. | m>-$\frac{4}{3}$ | C. | m>$\frac{4}{3}$ | D. | m<-$\frac{4}{3}$ |
19.二元一次方程x-2y=4( )
| A. | 有一个解且只有一个解 | B. | 无解 | ||
| C. | 有无数多个解 | D. | 有两个解且只有两个解 |
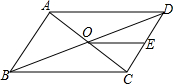 如图?ABCD中,AC、BD交于点O,E是CD边的中点,连接OE,若?ABCD周长为20,BD=8,则△ODE的周长为9.
如图?ABCD中,AC、BD交于点O,E是CD边的中点,连接OE,若?ABCD周长为20,BD=8,则△ODE的周长为9.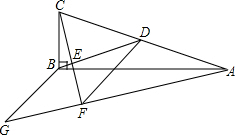 如图,在△ABC中,∠ABC=90°,点D为AC的中点,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
如图,在△ABC中,∠ABC=90°,点D为AC的中点,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.