题目内容
11.如图所示,有两种形状不同的直角三角形纸片各两块,其中一种纸片的两条直角边长都为3,另一种纸片的两条直角边长分别为1和3.图1、图2、图3是三张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长为1.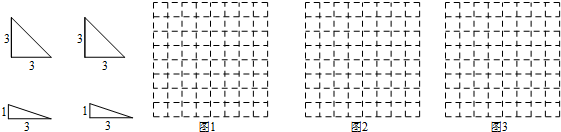
(1)请用三种方法(拼出的两个图形只要不全等就认为是不同的拼法)将图中所给四块直角三角形纸片拼成平行四边形(非矩形),每种方法要把图中所给的四块直角三角形纸片全部用上,互不重叠且不留空隙,并把你所拼得的图形按实际大小画在图1、图2、图3的方格纸上(要求:所画图形各顶点必须与方格纸中的小正方形顶点重合;画图时,要保留四块直角三角形纸片的拼接痕迹);
(2)三种方法所拼得的平行四边形的面积是否是定值?若是定值,请直接写出这个定值;若不是定值,请直接写出三种方法所拼得的平行四边形的面积各是多少;
(3)三种方法所拼得的平行四边形的周长是否是定值?若是定值,请直接写出这个定值;若不是定值,请直接写出三种方法所拼得的平行四边形的周长各是多少.
分析 (1)可以先用边长为1、3的直角三角形拼出矩形,再分别在边长为3的两侧拼上边长都为3的直角三角形;
(2)可以先用边长都为3的直角三角形拼出矩形,再分别在边长为3的两侧拼上边长都为3、1的直角三角形;
(3)以四个直角三角形的直角边拼出对角线为4的平行四边形即可.
解答 解:(1)3种拼法;
(2)三种方法所拼得的平行四边形的面积是定值,这个定值是12;
(3)三种方法所拼得的平行四边形的周长不是定值,
它们的周长分别是8+6$\sqrt{2}$,2$\sqrt{10}$+6$\sqrt{2}$,8+2$\sqrt{10}$.
点评 此题主要考查四边形综合题,其中涉及到了平行四边形的判定与性质,平行四边形的面积,灵活掌握平行四边形与三角形之间关系是解题的难点.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
19.二元一次方程x-2y=4( )
| A. | 有一个解且只有一个解 | B. | 无解 | ||
| C. | 有无数多个解 | D. | 有两个解且只有两个解 |
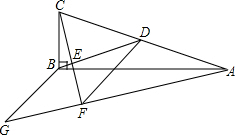 如图,在△ABC中,∠ABC=90°,点D为AC的中点,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
如图,在△ABC中,∠ABC=90°,点D为AC的中点,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.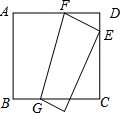 如图,将边长为12厘米的正方形ABCD折叠,使得A点落在CD上的E点,然后压平折痕FG,若FG的长为13厘米,则线段CE的长为( )
如图,将边长为12厘米的正方形ABCD折叠,使得A点落在CD上的E点,然后压平折痕FG,若FG的长为13厘米,则线段CE的长为( )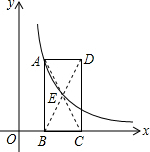 已知如图:矩形ABCD的边BC在x轴上,E为对角线AC、BD的交点,点B、D的坐标分别为B(1,0),D(3,3).
已知如图:矩形ABCD的边BC在x轴上,E为对角线AC、BD的交点,点B、D的坐标分别为B(1,0),D(3,3).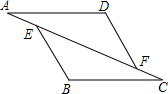 如图,△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:①AD=CB;②AE=CF;③∠B=∠D;④AD∥BC.请用其中三个作为条件,余下一个作为结论,使它组成一个真命题,并加以证明.
如图,△AFD和△BEC中,点A、E、F、C在同一直线上,有下面四个论断:①AD=CB;②AE=CF;③∠B=∠D;④AD∥BC.请用其中三个作为条件,余下一个作为结论,使它组成一个真命题,并加以证明. 已知点A(-1,0),B(3,0),C(4,2),D(0,4).
已知点A(-1,0),B(3,0),C(4,2),D(0,4).