题目内容
18. 钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10$\sqrt{2}$海里,求AC的距离.(结果保留根号)
钓鱼岛是我国的神圣领土,中国人民维护国家领土完整的决心是坚定的,多年来,我国的海监、渔政等执法船定期开赴钓鱼岛巡视.某日,我海监船(A处)测得钓鱼岛(B处)距离为20海里,海监船继续向东航行,在C处测得钓鱼岛在北偏东45°的方向上,距离为10$\sqrt{2}$海里,求AC的距离.(结果保留根号)
分析 作BD⊥AC交AC的延长线于D,根据正弦的定义求出BD、CD的长,根据勾股定理求出AD的长,计算即可.
解答 解: 作BD⊥AC交AC的延长线于D,
作BD⊥AC交AC的延长线于D,
由题意得,∠BCD=45°,BC=10$\sqrt{2}$海里,
∴CD=BD=10海里,
∵AB=20海里,BD=10海里,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=10$\sqrt{3}$,
∴AC=AD-CD=10$\sqrt{3}$-10海里.
答:AC的距离为(10$\sqrt{3}$-10)海里.
点评 本题考查的是解直角三角形的应用-方向角问题,熟记锐角三角函数的定义、正确标注方向角、正确作出辅助线是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
6. 如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,则树的高度AB为( )
如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,则树的高度AB为( )
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
 如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,则树的高度AB为( )
如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,则树的高度AB为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
| A. | 20m | B. | 15m | C. | 12m | D. | 16m |
3. 从如图所示的四个带圆圈的数字中,任取两个数字(既可以是相邻也可以是相对的两个数字)相互交换它们的位置,交换一次后能使①、②两数在相对位置上的概率是( )
从如图所示的四个带圆圈的数字中,任取两个数字(既可以是相邻也可以是相对的两个数字)相互交换它们的位置,交换一次后能使①、②两数在相对位置上的概率是( )
 从如图所示的四个带圆圈的数字中,任取两个数字(既可以是相邻也可以是相对的两个数字)相互交换它们的位置,交换一次后能使①、②两数在相对位置上的概率是( )
从如图所示的四个带圆圈的数字中,任取两个数字(既可以是相邻也可以是相对的两个数字)相互交换它们的位置,交换一次后能使①、②两数在相对位置上的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
10. 如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
 如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
7.比较a与-a的大小( )
| A. | a>-a | B. | a<-a | C. | a=-a | D. | 以上都有可能 |
 雨伞的中截图如图所示,伞背AB=AC,支撑杆OE=OF,AE=$\frac{1}{4}$AB,AF=$\frac{1}{4}$AC,当O沿AD滑动时,雨伞开闭;问雨伞开闭过程中,∠BEO与∠CFO有何关系?说明理由.
雨伞的中截图如图所示,伞背AB=AC,支撑杆OE=OF,AE=$\frac{1}{4}$AB,AF=$\frac{1}{4}$AC,当O沿AD滑动时,雨伞开闭;问雨伞开闭过程中,∠BEO与∠CFO有何关系?说明理由.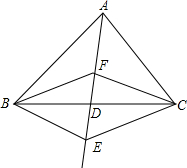 如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE.
如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE.