题目内容
15.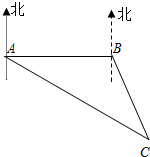 如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)
如图,专业救助船“沪救1”轮、“沪救2”轮分别位于A、B两处,同时测得事发地点C在A的南偏东60°且C在B的南偏东30°上.已知B在A的正东方向,且相距100里,请分别求出两艘船到达事发地点C的距离.(注:里是海程单位,相当于一海里.结果保留根号)
分析 作BG⊥AC于G,在图中标注方向角,根据等腰三角形的性质和正弦、余弦的概念求出AC、BC即可.
解答 解: 作BG⊥AC于G,
作BG⊥AC于G,
∵点C在A的南偏东60°,
∴∠A=90°-60°=30°,
∵C在B的南偏东30°,
∴∠ABC=120°,
∴∠C=30°,
∴BC=AB=100里,
∴BG=BC•sin30°=50里,
CG=BC•cos30°=50$\sqrt{3}$里,
∴AC=2CG=100$\sqrt{3}$里.
答:A船到达事发地点C的距离是100$\sqrt{3}$里,B船到达事发地点C的距离是100里.
点评 本题考查的是解直角三角形的应用-方向角问题,正确标注方向角、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
相关题目
13.若点P(m+5,2)与点Q(3,n-5)关于y轴对称,则m,n的值分别是( )
| A. | -8,-7 | B. | 8,-7 | C. | -8,7 | D. | 8,7 |
6. 如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,则树的高度AB为( )
如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,则树的高度AB为( )
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
 如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,则树的高度AB为( )
如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,则树的高度AB为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
| A. | 20m | B. | 15m | C. | 12m | D. | 16m |
3. 从如图所示的四个带圆圈的数字中,任取两个数字(既可以是相邻也可以是相对的两个数字)相互交换它们的位置,交换一次后能使①、②两数在相对位置上的概率是( )
从如图所示的四个带圆圈的数字中,任取两个数字(既可以是相邻也可以是相对的两个数字)相互交换它们的位置,交换一次后能使①、②两数在相对位置上的概率是( )
 从如图所示的四个带圆圈的数字中,任取两个数字(既可以是相邻也可以是相对的两个数字)相互交换它们的位置,交换一次后能使①、②两数在相对位置上的概率是( )
从如图所示的四个带圆圈的数字中,任取两个数字(既可以是相邻也可以是相对的两个数字)相互交换它们的位置,交换一次后能使①、②两数在相对位置上的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
10. 如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
 如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
7.比较a与-a的大小( )
| A. | a>-a | B. | a<-a | C. | a=-a | D. | 以上都有可能 |
5.实数$\sqrt{2}+1$是( )
| A. | 整数 | B. | 分数 | C. | 有理数 | D. | 无理数 |
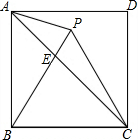 如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点E.有以下结论:
如图,点P在正方形ABCD内,△PBC是正三角形,AC与PB相交于点E.有以下结论: