题目内容
5. 在一山顶有铁塔AB,从点P到铁塔底部B点有一条索道PB,索道长为300米,与水平线成角为α=30°,在P处测得A点的仰角为β=45°,试求铁塔的高AB.(精确到0.1米,其中$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
在一山顶有铁塔AB,从点P到铁塔底部B点有一条索道PB,索道长为300米,与水平线成角为α=30°,在P处测得A点的仰角为β=45°,试求铁塔的高AB.(精确到0.1米,其中$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
分析 根据正弦、余弦的定义分别求出BC、PC的长,根据AB=AC-BC计算即可.
解答 解: 由题意得,PB=300米,∠BPC=30°,
由题意得,PB=300米,∠BPC=30°,
∴BC=PB•sin∠BPC=150米,PC=PB•cos∠BPC=150$\sqrt{3}$≈259.5米,
∵∠APC=45°,
∴AC=PC=259.5米,
∴AB=AC-BC=109.5米.
答:铁塔的高AB约为109.5米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,熟记锐角三角函数的定义、理解仰角俯角的概念是解题的关键.

练习册系列答案
相关题目
3.将下列长度的三根木棒首尾顺次连接,能组成三角形的是( )
| A. | 1,2,4 | B. | 8,6,4 | C. | 12,6,5 | D. | 3,3,6 |
20. 如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
 如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )
如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1等于( )| A. | 132° | B. | 134° | C. | 136° | D. | 138° |
10. 如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
 如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
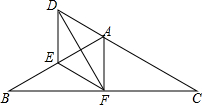 如图,△ABC中,AB=AC=6,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.
如图,△ABC中,AB=AC=6,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.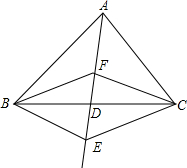 如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE.
如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE. 如图所示,两个紧靠在一起的圆柱体组成的物体,它的主视图是( )
如图所示,两个紧靠在一起的圆柱体组成的物体,它的主视图是( )



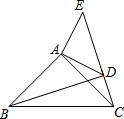 如图,△ACB和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连结BD.求证:
如图,△ACB和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,点C、D、E三点在同一直线上,连结BD.求证: