题目内容
16．
已知如图，在?ABCD中，BF⊥AD、BE⊥DC，垂足分别是F、E，∠EDF=30°，BE=8，BF=14，则?ABCD的周长是88．
分析 由在?ABCD中，BF⊥AD、BE⊥DC，∠EDF=30°，易得△ABF与△BCE是含30°的直角三角形，继而求得AB与BC的长，进而求得?ABCD的周长．
解答 解：∵四边形ABCD是平行四边形，
∴AB∥CD，∠A=∠C，
∴∠A=∠EDF=30°，
∴∠C=30°，
∵BF⊥AD，BE⊥DC，BF=14，BE=8，
∴AB=2BF=28，BC=2BE=16，
∴?ABCD的周长是：2（AB+BC）=88．
故答案为：88．
点评 此题考查了平行四边形的性质以及含30°的直角三角形的性质．注意求得△ABF与△BCE是含30°的直角三角形是关键．
练习册系列答案
新思维寒假作业系列答案
相关题目
如图，将一张长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置上，ED′的延长线与BC的交点为G，若∠EFG=56°，则∠2-∠1=44°．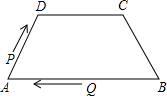
如图，在四边形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=11，点P从点A出发，以3个单位/s的速度沿AD→DC向终点C运动，同时点Q从点B出发，以1个单位/s的速度沿BA向终点A运动，在运动期间，当四边形PQBC为平行四边形时，运动时间为3秒．
11．
如图，将周长为10的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长为（ ）
如图，将周长为10的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长为（ ）| A． | 8 | B． | 10 | C． | 12 | D． | 14 |