题目内容
9.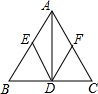 如图,在△ABC中,点D是BC的中点,DE∥AC,DF∥AB.
如图,在△ABC中,点D是BC的中点,DE∥AC,DF∥AB.(1)当△ABC满足什么条件时,四边形AEDF是菱形?并说明理由.
(2)当△ABC满足什么条件时,四边形AEDF是正方形?(直接写出答案)
分析 (1)先证明四边形AEDF是平行四边形,再证出∠FDA=∠FAD,得出AF=DF,即可得出结论.
(2)根据有一个角是直角的菱形是正方形可得△ABC是等腰直角三角形时,四边形AEDF是正方形.
解答 解:(1)当AB=AC时,四边形AEDF是菱形;理由如下:
∵DE∥AC,DF∥AB,
∴DE∥AF,DF∥AE,
∴四边形AEDF是平行四边形,∠EAD=∠FDA;
∵AD⊥BC,AB=AC,
∴AD是∠BAC的平分线,
∴∠EAD=∠FAD,
∴∠FDA=∠FAD,
∴AF=DF(等角对等边),
∴四边形AEDF是菱形(一组邻边相等的平行四边形是菱形).
(2)当△ABC是等腰直角三角形时,四边形AEDF是正方形.
由(1)可得:当AB=AC时,四边形AEDF是菱形,
∵∠BAC=90°,
∴四边形AEDF是正方形(有一个角是直角的菱形是正方形).
点评 此题主要考查了菱形的判定和正方形的判定,关键是掌握邻边相等的平行四边形是菱形,有一个角是直角的菱形是正方形.

练习册系列答案
相关题目
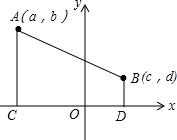 已知,如图,点A(a,b),B(c,d)在平面直角坐标系中的任意两点,且AC⊥x轴于点C,BD⊥x轴于点D.
已知,如图,点A(a,b),B(c,d)在平面直角坐标系中的任意两点,且AC⊥x轴于点C,BD⊥x轴于点D.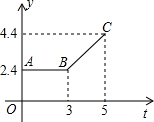 如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.
如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.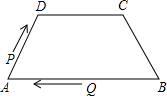 如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=11,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.
如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=11,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.