题目内容
5．已知a、b、c为实数，且（a-c）2＞a2+c2，则关于x的方程ax2+bx+c=0根的情况是（ ）| A． | 有两个相等的实数根 | B． | 无实数根 | ||
| C． | 有两个不相等的实数根 | D． | 有一根为0 |
分析 根据不等式（a-c）2＞a2+c2，可求出ac＜0，再根据方程ax2+bx+c=0的根的判别式△=b2-4ac，由此即可得出△＞0，即方程有两个不相等的实数根．
解答 解：∵（a-c）2=a2+c2-2ac＞a2+c2，
∴ac＜0．
在方程ax2+bx+c=0中，△=b2-4ac，
∵b2≥0，ac＜0，
∴△=b2-4ac＞0，
∴方程ax2+bx+c=0有两个不相等的实数根．
故选C．
点评 本题考查了根的判别式以及解不等式，通过解不等式找出ac＜0是解题的关键．
练习册系列答案
智能训练练测考系列答案
计算高手系列答案
相关题目
17．抛物线y=（x-m）2+n可以由抛物线y=x2向上平移2个单位，再向左平移3个单位得到，则m-n值为（ ）
| A． | -6 | B． | -5 | C． | -1 | D． | 1 |
14．
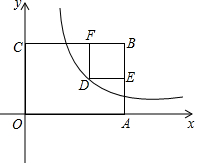如图，矩形OABC的顶点B（7，6），顶点A、C在坐标轴上，矩形内部一点D在双曲线y=$\frac{12}{x}$上，DE⊥AB于点E，DF⊥BC于点F，若四边形DEBF为正方形，则点D的坐标是（ ）
如图，矩形OABC的顶点B（7，6），顶点A、C在坐标轴上，矩形内部一点D在双曲线y=$\frac{12}{x}$上，DE⊥AB于点E，DF⊥BC于点F，若四边形DEBF为正方形，则点D的坐标是（ ）| A． | （2，6） | B． | （3，4） | C． | （4，3） | D． | （6，2） |