题目内容
13.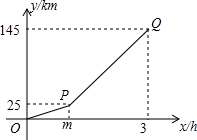 甲、乙两地相距145km,小李骑摩托车从甲地出发去往乙地,速度为25km/h,中途因故换成汽车继续前往乙地(换车时间忽略不计),小李与甲地的距离y(单位:km)和所用时间x(单位:h)之间的关系如图所示.
甲、乙两地相距145km,小李骑摩托车从甲地出发去往乙地,速度为25km/h,中途因故换成汽车继续前往乙地(换车时间忽略不计),小李与甲地的距离y(单位:km)和所用时间x(单位:h)之间的关系如图所示.(1)小李骑摩托车所用的时间m=1,汽车的速度是60km/h;
(2)当m≤x≤3时,求y关于x的函数解析式.
分析 (1)利用小李骑摩托车的速度以及其行驶的路程得出m的值,再利用甲、乙两地相距145km,再结合行驶时间得出汽车的速度;
(2)首先得出P,Q点坐标,进而利用待定系数法求出一次函数解析式.
解答 解:(1)由题意可得:小李骑摩托车所用的时间m=25÷25=1(h),
汽车的速度是:(145-25)÷(3-1)=60(km/h);
故答案为:1,60;
(2)当m≤x≤3时,设y关于x的函数关系式为:y=kx+b,
由题可得:m=1,P(1,25),Q(3,145),
把P,Q两点坐标代入:y=kx+b,
得:$\left\{\begin{array}{l}{25=k+b}\\{145=3k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=60}\\{b=-35}\end{array}\right.$,
故y关于x的函数解析式为:y=60x-35.
点评 此题主要考查了一次函数的应用,利用图象得出正确信息是解题关键.

练习册系列答案
相关题目
18.下列式子中,表示y是x的正比例函数的是( )
| A. | y=x+5 | B. | y=3x | C. | y=3x2 | D. | y2=3x |
1.近似数3.14×104的精确到( )
| A. | 个位 | B. | 百位 | C. | 百分位 | D. | 千位 |
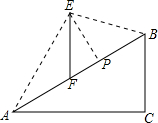 如图,在坡度i=1:$\sqrt{3}$的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为( )(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,在坡度i=1:$\sqrt{3}$的斜坡AB上立有一电线杆EF,工程师在点A处测得E的仰角为60°,沿斜坡前进20米到达B,此时测得点E的仰角为15°,现要在斜坡AB上找一点P,在P处安装一根拉绳PE来固定电线杆,以使EF保持竖直,为使拉绳PE最短,则FP的长度约为( )(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)