题目内容
 已知,AB是⊙O的直径,AD、BC是⊙O的切线,AB=4,AD=3,BC=6.
已知,AB是⊙O的直径,AD、BC是⊙O的切线,AB=4,AD=3,BC=6.(1)求CD的长;
(2)点C、D分别沿射线CB、DA方向同时以每秒1个单位长度的速度运动,运动多长时间线段CD恰好与⊙O相切?
(3)点P为⊙O上任一点,求△PCD面积的最大值.
考点:切线的判定,切线的性质
专题:计算题
分析:(1)作DE⊥BC于E,如图1,根据切线的性质得AB⊥AD,AB⊥BC,则肯定判断四边形ABED为矩形,所以DE=AB=4,BE=AD=3,CE=BC-BE=3,然后在Rt△CDE中利用勾股定理计算出CD=5;
(2)设两点运动的时间为t,分类讨论:如图2,当点C、点D分别运动到N、M的位置与⊙O相切于Q,则MD=CN=t,易得四边形CNMD为平行四边形,则MN=CD=5,作MH⊥BC于H,则MH=AB=4,在Rt△MNH中计算出NH=3,设AM=x,利用切线长定理得MA=MQ=x,NQ=NB=NH+BH,加上AM=BH=x,则x+3+x=5,解得x=1,所以AM=1,MD=AD-AM=2,于是得到此时两点运动的时间为2s;当点C、点D分别运动到F、E的位置与⊙O相切于P,同理可得BF=1,CF=BC+BF=7,得到此时两点运动的时间为7s;
(3)点P为EF与⊙O的切点时,由于点P到CD的距离最大,所以此时△PCD面积的最大值,然后利用S△PDC=
S平行四边形CDEF进行计算,
(2)设两点运动的时间为t,分类讨论:如图2,当点C、点D分别运动到N、M的位置与⊙O相切于Q,则MD=CN=t,易得四边形CNMD为平行四边形,则MN=CD=5,作MH⊥BC于H,则MH=AB=4,在Rt△MNH中计算出NH=3,设AM=x,利用切线长定理得MA=MQ=x,NQ=NB=NH+BH,加上AM=BH=x,则x+3+x=5,解得x=1,所以AM=1,MD=AD-AM=2,于是得到此时两点运动的时间为2s;当点C、点D分别运动到F、E的位置与⊙O相切于P,同理可得BF=1,CF=BC+BF=7,得到此时两点运动的时间为7s;
(3)点P为EF与⊙O的切点时,由于点P到CD的距离最大,所以此时△PCD面积的最大值,然后利用S△PDC=
| 1 |
| 2 |
解答: 解:(1)作DE⊥BC于E,如图1,
解:(1)作DE⊥BC于E,如图1,
∵AB是⊙O的直径,AD、BC是⊙O的切线,
∴AB⊥AD,AB⊥BC,
∴四边形ABED为矩形,
∴DE=AB=4,BE=AD=3,
∴CE=BC-BE=6-3=3,
在Rt△CDE中,∵CE=3,DE=4,
∴CD=
=5;
(2)设两点运动的时间为t,
如图2当点C、点D分别运动到N、M的位置与⊙O相切于Q,则MD=CN=t
∵DM∥CN,
∴四边形CNMD为平行四边形,
∴MN=CD=5,
作MH⊥BC于H,则MH=AB=4,
在Rt△MNH中,∵MN=5,MH=4,
∴NH=
=3,
设AM=x
∵MA=MQ=x,NQ=NB=NH+BH,
而AM=BH=x,
∴x+3+x=5,解得x=1,
∴AM=1,
∴MD=AD-AM=2,
∴此时两点运动的时间为2s;
当点C、点D分别运动到F、E的位置与⊙O相切于P,同理可得BF=1,
∴CF=BC+BF=7,
∴此时两点运动的时间为7s;
综上所述,运动2s或7s时间线段CD恰好与⊙O相切;
(3)点P为EF与⊙O的切点时,△PCD面积的最大值,
此时S△PDC=
S平行四边形CDEF=
•4•7=14,
即△PCD面积的最大值为14.
 解:(1)作DE⊥BC于E,如图1,
解:(1)作DE⊥BC于E,如图1,∵AB是⊙O的直径,AD、BC是⊙O的切线,
∴AB⊥AD,AB⊥BC,
∴四边形ABED为矩形,
∴DE=AB=4,BE=AD=3,
∴CE=BC-BE=6-3=3,
在Rt△CDE中,∵CE=3,DE=4,
∴CD=
| CE2+DE2 |
(2)设两点运动的时间为t,
如图2当点C、点D分别运动到N、M的位置与⊙O相切于Q,则MD=CN=t
∵DM∥CN,
∴四边形CNMD为平行四边形,
∴MN=CD=5,
作MH⊥BC于H,则MH=AB=4,
在Rt△MNH中,∵MN=5,MH=4,
∴NH=
| MN2-MH2 |

设AM=x
∵MA=MQ=x,NQ=NB=NH+BH,
而AM=BH=x,
∴x+3+x=5,解得x=1,
∴AM=1,
∴MD=AD-AM=2,
∴此时两点运动的时间为2s;
当点C、点D分别运动到F、E的位置与⊙O相切于P,同理可得BF=1,
∴CF=BC+BF=7,
∴此时两点运动的时间为7s;
综上所述,运动2s或7s时间线段CD恰好与⊙O相切;
(3)点P为EF与⊙O的切点时,△PCD面积的最大值,
此时S△PDC=
| 1 |
| 2 |
| 1 |
| 2 |
即△PCD面积的最大值为14.
点评:本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.在判定一条直线为圆的切线时,当已知条件中未明确指出直线和圆是否有公共点时,常过圆心作该直线的垂线段,证明该线段的长等于半径;当已知条件中明确指出直线与圆有公共点时,常连接过该公共点的半径,证明该半径垂直于这条直线.也考查了切线的性质和切线长定理.

练习册系列答案
相关题目
每天早上7点45分我们开始第一节课,此时钟表上分针与时针的夹角是( )
| A、60° | B、45° |
| C、37.5° | D、35.° |
在平面直角坐标系中,(m+2,n-1)与(4,3)关于y轴对称,那么2m+n=( )
| A、-15 | B、-12 |
| C、-9 | D、-8 |
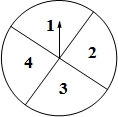 如图,是一个可以自由转动的转盘,转盘被平均分成四个相同的扇形,分别写有1、2、3、4四个数字,指针位置固定,转动转盘后任其自由停止(指针指向边界时重转),现转动转盘两次,请用画树形图法或列表法求出指针指向相同数字的概率.
如图,是一个可以自由转动的转盘,转盘被平均分成四个相同的扇形,分别写有1、2、3、4四个数字,指针位置固定,转动转盘后任其自由停止(指针指向边界时重转),现转动转盘两次,请用画树形图法或列表法求出指针指向相同数字的概率. 已知:△ABC中AC=mAB,点D是AB的中点,∠C+∠EDF=180°,DE、DF分别交AC、BC于E、F.
已知:△ABC中AC=mAB,点D是AB的中点,∠C+∠EDF=180°,DE、DF分别交AC、BC于E、F.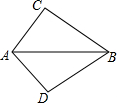 如图,已知∠ACB=∠ADB=90°,欲说明BC=BD,可补充条件
如图,已知∠ACB=∠ADB=90°,欲说明BC=BD,可补充条件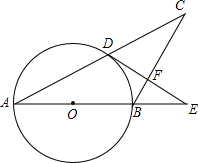 如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作DF⊥BC,交AB的延长线于E,垂足为F.
如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作DF⊥BC,交AB的延长线于E,垂足为F.