题目内容
1．
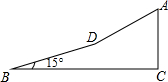如图，某校八年级（1）班学生利用寒假期间到郊区进行社会实践活动，活动之余，同学们准备攀登附近的一个小山坡，从B点出发，沿坡脚15°的坡面以5千米/时的速度行至D点，用了10分钟，然后沿坡比为1：$\sqrt{3}$的坡面以3千米/时的速度达到山顶A点，用了5分钟，求小山坡的高（即AC的长度）（精确到0.01千米）（sin15°≈0.2588，cos15°≈0.9659，$\sqrt{3}$≈1.732）
分析 过点D作DF⊥BC于F，DE⊥AC于点E，分别利用坡角及三角函数求出AE，DF的值即可求得AC的长．
解答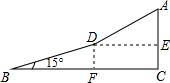 
解：过D作DF⊥BC于F，DE⊥AC于点E，
∵沿坡比为1：$\sqrt{3}$的坡面以3千米/时的速度达到山顶A点，
∴$\frac{AE}{DE}$=$\frac{1}{\sqrt{3}}$，
∴∠ADE=30°，
∵BD=$\frac{5}{60}$×10=$\frac{5}{6}$（km），AD=$\frac{3}{60}$×5=$\frac{1}{4}$（km），
∴AC=AE+EC=AE+DF=AD•sin30°+BD•sin15°=$\frac{1}{4}$×$\frac{1}{2}$+$\frac{5}{6}$×0.2588≈0.34（千米）．
答：小山坡的高为0.34千米．
点评 此题主要考查了坡度坡角问题以及及三角函数的综合运用，正确应用锐角三角函数关系是解题关键．
练习册系列答案
优翼小帮手同步口算系列答案
相关题目
11．
如图，平行四边形ABCD的对角线AC、BD相交于点O，则下列说法一定正确的（ ）
如图，平行四边形ABCD的对角线AC、BD相交于点O，则下列说法一定正确的（ ）| A． | AO=OD | B． | AO⊥OD | C． | AO=OC | D． | AO⊥AB |
16．方程组$\left\{\begin{array}{l}{x-y=1}\\{2x+y=5}\end{array}\right.$的解是（ ）
| A． | $\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ |
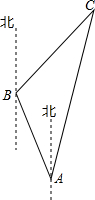为有效开发海洋资源，保护海洋权益，我国对南海诸岛进行了全面调查，一测量船在A岛测得B岛在北偏西30°，C岛在北偏东15°，航行100海里到达B岛，在B岛测得C岛在北偏东45°，求B，C两岛及A，C两岛的距离（$\sqrt{6}$≈2.45，结果保留到整数）