题目内容
17.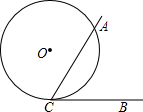 如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )
如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )| A. | $\sqrt{3}$ | B. | $\frac{1}{3}\sqrt{3}$ | C. | π 或$\sqrt{3}$ | D. | $\frac{1}{3}\sqrt{3}$或$\sqrt{3}$ |
分析 根据题意画图,当圆O滚动到圆W位置与CA,CB相切,切点分别为E,F,连接WE,WF,CW,OC,OW,则四边形OWC是矩形;构造直角三角形利用直角三角形中的30°角的三角函数值,可求得点O移动的距离为OW=CF=WF•cot∠WCF=WF•cot30°=$\sqrt{3}$.
解答  解:①如图1,当圆O滚动到圆W位置与CA,CB相切,切点分别为E,F,
解:①如图1,当圆O滚动到圆W位置与CA,CB相切,切点分别为E,F,
连接WE,WF,CW,OC,OW,则OW=CF,WF=1,∠WCF=$\frac{1}{2}$∠ACB=30°,
所以点O移动的距离为OW=CF=WF•cot∠WCF=WF•cot30°=$\sqrt{3}$.
②如图2,当圆O滚动到圆O′位置与CA,CB相切,切点分别为F,E,
连接OO′,O′E,O′C,O′F,OC,
则OO′=CE,∠O′CE=60°,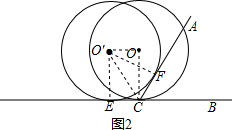
∴点O移动的距离为OO′=O′E•cot60°=$\frac{\sqrt{3}}{3}$,
综上所述:滚动到⊙O与CA也相切时,圆心O移动的水平距离为:$\sqrt{3}$或$\frac{\sqrt{3}}{3}$,
故选D.
点评 此题考查了切线的性质与切线长定理,以及三角函数等知识.解此题的关键是根据题意作出图形,注意数形结合思想的应用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
8.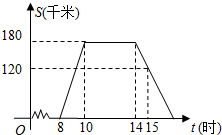 端午节三天假期的某一天,小明全家上午8时自架小汽车从家里出发,到某著名旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.根据图象提供的有关信息,下列说法中错误的是( )
端午节三天假期的某一天,小明全家上午8时自架小汽车从家里出发,到某著名旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.根据图象提供的有关信息,下列说法中错误的是( )
 端午节三天假期的某一天,小明全家上午8时自架小汽车从家里出发,到某著名旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.根据图象提供的有关信息,下列说法中错误的是( )
端午节三天假期的某一天,小明全家上午8时自架小汽车从家里出发,到某著名旅游景点游玩.该小汽车离家的距离S(千米)与时间t(小时)的关系如图所示.根据图象提供的有关信息,下列说法中错误的是( )| A. | 景点离小明家180千米 | B. | 小明到家的时间为17点 | ||
| C. | 返程的速度为60千米每小时 | D. | 10点至14点,汽车匀速行驶 |


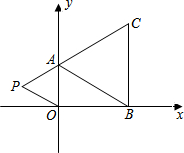 如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0,c=2b-a
如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0,c=2b-a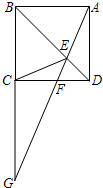 如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F,则:①四边形ABCD是正方形;②△CEG∽△FEC;③C是BG的中点;④当AE=2EF时,FG=3EF,正确的有几个( )
如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F,则:①四边形ABCD是正方形;②△CEG∽△FEC;③C是BG的中点;④当AE=2EF时,FG=3EF,正确的有几个( )