题目内容
2.解不等式组$\left\{\begin{array}{l}{\frac{x-6}{3}<\frac{1}{4}}\\{3(6-x)≤9}\end{array}\right.$.分析 先分别解两个不等式得到x<$\frac{27}{4}$和x≥3,然后根据大于小的小于大的取中间即可确定不等式组的解集.
解答 解:解不等式①得:x<$\frac{27}{4}$,
解不等式②得:x≥3,
故不等式组得解集为3≤x<$\frac{27}{4}$.
点评 本题考查了解一元一次不等式组:求解出两个不等式的解集,然后按照“同大取大,同小取小,大于小的小于大的取中间,小于小的大于大的无解”确定不等式组的解集.

练习册系列答案
相关题目
13.已知实数x,y,z满足$\left\{\begin{array}{l}{x+y+z=5}\\{4x+y-2z=2}\end{array}\right.$,则代数式4x-4z+1的值是( )
| A. | -3 | B. | 3 | C. | -7 | D. | 7 |
10.已知关于x的不等式组$\left\{\begin{array}{l}{x-m≥n}\\{2x-m<2n+1}\end{array}\right.$的解集为3≤x<5,则m-n的值是( )
| A. | -9 | B. | 9 | C. | 5 | D. | -5 |
17.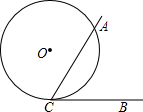 如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )
如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )
 如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )
如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )| A. | $\sqrt{3}$ | B. | $\frac{1}{3}\sqrt{3}$ | C. | π 或$\sqrt{3}$ | D. | $\frac{1}{3}\sqrt{3}$或$\sqrt{3}$ |
14.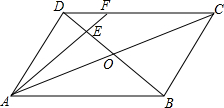 如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△BAE=( )
如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△BAE=( )
 如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△BAE=( )
如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△BAE=( )| A. | 1:4 | B. | 1:3 | C. | 1:8 | D. | 1:9 |
11. 某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )
某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )
 某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )
某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )| A. | 每月阅读数量的平均数是50 | B. | 众数是42 | ||
| C. | 中位数是58 | D. | 每月阅读数量超过40的有4个月 |
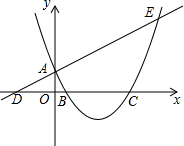 如图,已知直线y=$\frac{1}{2}$x+1与y轴交于点A,与x轴交于点D,抛物线y=$\frac{1}{2}$x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).
如图,已知直线y=$\frac{1}{2}$x+1与y轴交于点A,与x轴交于点D,抛物线y=$\frac{1}{2}$x2+bx+c与直线交于A、E两点,与x轴交于B、C两点,且B点坐标为(1,0).