题目内容
6.在平面直角坐标系中,点O为原点,抛物线y=ax2+bx(其中-1≤a<0)经过A(3,n),AB⊥y轴于B,抛物线交直线AB于M.(1)若n=1,AB=3BM,求抛物线所对应的函数关系式;
(2)若n=a+b,抛物线与x轴另一个异于原点的交点为C,过点A作AP∥OM交直线MC于点P,当△OPM的面积最大时,求sin∠MOP的值.
分析 (1)先利用AB=3,AB=3BM得到BM=1,则M(1,1),A(3,1),然后把M点和A点坐标代入y=ax2+bx得到关于a和b的方程组,再解方程组求出a和b即可得到抛物线所对应的函数关系式;
(2)先把A(3,a+b)代入y=ax2+bx可得b=-4a,则抛物线解析式为y=ax2-4ax,A(3,-3a),利用抛物线与x轴的交点问题可求出C(4,0),则抛物线的对称轴为直线x=2,利用抛物线的对称性得到M(1,-3a),由于AP∥OM,根据三角形面积公式有S△OMP=S△OMA=$\frac{1}{2}$×2×(-3a)=-3a,而-1≤a<0,所以a=-1时,△OPM面积的最大值为3,此时M(1,3),A(3,3),接着利用待定系数法求出直线MC的解析式为y=-x+4,直线OM的解析式为y=3x,直线AP的解析式为y=3x-6,通过解方程组$\left\{\begin{array}{l}{y=-x+4}\\{y=3x-6}\end{array}\right.$得P($\frac{5}{2}$,$\frac{3}{2}$),则可利用勾股定理计算出OP=$\frac{\sqrt{34}}{2}$,作PH⊥OM于H,如图,由于OM=$\sqrt{10}$,S△OMP=3,则利用三角形公式可计算出PH=$\frac{3\sqrt{10}}{5}$,然后在Rt△OPH中,利用正弦的定义求解.
解答 解:(1)∵A(3,n),
∴AB=3,
∵AB=3BM,
∴BM=1,
∵n=1,
∴M(1,1),A(3,1),
把M(1,1),A(3,1)代入y=ax2+bx得$\left\{\begin{array}{l}{a+b=1}\\{9a+3b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{1}{3}}\\{b=\frac{4}{3}}\end{array}\right.$,
∴抛物线所对应的函数关系式为y=-$\frac{1}{3}$x2+$\frac{4}{3}$x;
(2)把A(3,a+b)代入y=ax2+bx得9a+3b=a+b,则b=-4a,
∴抛物线解析式为y=ax2-4ax,A(3,-3a),
当y=0时,ax2-4ax=0,解得x1=0,x2=4,则C(4,0),
∴抛物线的对称轴为直线x=2,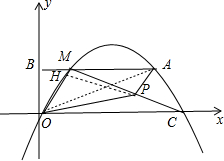
∵点A与点M关于直线x=2对称,
∴M(1,-3a),
∵AP∥OM,
∴S△OMP=S△OMA=$\frac{1}{2}$×2×(-3a)=-3a,
而-1≤a<0,
∴当△OPM的面积最大时,a=-1,
即a=-1时,△OPM的面积为3,
∴M(1,3),A(3,3),
设直线MC的解析式为y=kx+m,
把M(1,3),C(4,0)代入得$\left\{\begin{array}{l}{k+m=3}\\{4k+m=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{m=4}\end{array}\right.$,
∴直线MC的解析式为y=-x+4,
易得直线OM的解析式为y=3x,
∵AP∥MO,
∴设直线AP的解析式为y=3x+p,
把A(3,3)代入得9+p=3,解得p=-6,
∴直线AP的解析式为y=3x-6,
解方程组$\left\{\begin{array}{l}{y=-x+4}\\{y=3x-6}\end{array}\right.$得$\left\{\begin{array}{l}{x=\frac{5}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,则P($\frac{5}{2}$,$\frac{3}{2}$),
∴OP=$\sqrt{(\frac{5}{2})^{2}+(\frac{3}{2})^{2}}$=$\frac{\sqrt{34}}{2}$,
作PH⊥OM于H,如图,
∵OM=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,S△OMP=3,
∴$\frac{1}{2}$×$\sqrt{10}$×PH=3,
∴PH=$\frac{3\sqrt{10}}{5}$,
在Rt△OPH中,sin∠HOP=$\frac{PH}{OP}$=$\frac{\frac{3\sqrt{10}}{5}}{\frac{\sqrt{34}}{2}}$=$\frac{6\sqrt{85}}{85}$,
即sin∠MOP=$\frac{6\sqrt{85}}{85}$.
点评 本题考查了二次函数的综合题:熟练掌握二次函数的性质、抛物线与x轴的交点问题和两直线平行或相交的问题;会利用待定系数法求一次函数与二次函数的解析式;理解坐标与图形性质.解这类问题关键是善于将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识,并注意挖掘题目中的一些隐含条件.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案| A. | 16个 | B. | 20个 | C. | 25个 | D. | 30个 |
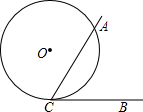 如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )
如图,∠ACB=60○,半径为1的⊙O切BC于点C,若将⊙O在直线CB上沿某一方向滚动,当滚动到⊙O与CA也相切时,圆心O移动的水平距离为( )| A. | $\sqrt{3}$ | B. | $\frac{1}{3}\sqrt{3}$ | C. | π 或$\sqrt{3}$ | D. | $\frac{1}{3}\sqrt{3}$或$\sqrt{3}$ |
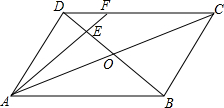 如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△BAE=( )
如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则S△DEF:S△BAE=( )| A. | 1:4 | B. | 1:3 | C. | 1:8 | D. | 1:9 |
| A. | y=2(x+1)2+3 | B. | y=-x2+4x+1 | C. | y=2x2+4x-3 | D. | y=-2x2-x+5 |
 某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )
某班班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线 统计图,下列说法正确的是( )| A. | 每月阅读数量的平均数是50 | B. | 众数是42 | ||
| C. | 中位数是58 | D. | 每月阅读数量超过40的有4个月 |
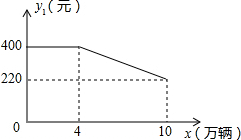 “低碳生活”作为一种健康、环保、安全的生活方式,受到越来越多人的关注.某公司生产的健身自行车在市场上受到普遍欢迎,在国内市场和国外市场畅销,生产的产品可以全部售出,在国内市场每辆的利润y1(元)与销量x(万辆)的关系如图所示;在国外市场每辆的利润y2 (元)与销量x(万量)的关系为:
“低碳生活”作为一种健康、环保、安全的生活方式,受到越来越多人的关注.某公司生产的健身自行车在市场上受到普遍欢迎,在国内市场和国外市场畅销,生产的产品可以全部售出,在国内市场每辆的利润y1(元)与销量x(万辆)的关系如图所示;在国外市场每辆的利润y2 (元)与销量x(万量)的关系为: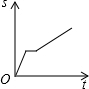
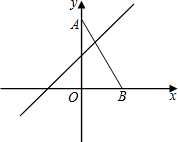 已知平面直角坐标系中,O为坐标原点,点A坐标为(0,8),点B坐标为(4,0),点E是直线y=x+4上的一个动点,若∠EAB=∠ABO,则点E的坐标为(4,8)或(-12,-8).
已知平面直角坐标系中,O为坐标原点,点A坐标为(0,8),点B坐标为(4,0),点E是直线y=x+4上的一个动点,若∠EAB=∠ABO,则点E的坐标为(4,8)或(-12,-8).