题目内容
(1)如果x2+x-1=0,则x3+2x2+3= .
(2)把(x2-x+1)6展开后得a12x12+a11x11+…+a2x2+a1x+a0,则a12+a10+a8+a6+a4+a2+a0= .
(2)把(x2-x+1)6展开后得a12x12+a11x11+…+a2x2+a1x+a0,则a12+a10+a8+a6+a4+a2+a0=
考点:因式分解的应用,代数式求值
专题:因式分解
分析:(1)把高次项用低次多项式表示,进行因式分解,再求值;(2)我们很难将(x2一x+1)6的展开式写出,因此想通过展开式去求出每一个系数是不实际的,事实上,上列等式在x的允许值范围内取任何一个值代入计算,等式都成立,考虑用赋值法解.
解答:解:(1)∵x2+x-1=0,
∴x2=1-x,
∴x3+2x2+3=x(1-x)+2x2+3=x2+x+3=1-x+x+3=4;
(2)令x=1,由已知等式得a12+a11+…+a2+a1+a0=1,①
令x=-1,得a12-a11+…+a2-a1+a0=729,②
①+②得2(a12+a10+a8+a6+a4+a2+a0)=730.
故a12+a10+a8+a6+a4+a2+a0=365.
∴x2=1-x,
∴x3+2x2+3=x(1-x)+2x2+3=x2+x+3=1-x+x+3=4;
(2)令x=1,由已知等式得a12+a11+…+a2+a1+a0=1,①
令x=-1,得a12-a11+…+a2-a1+a0=729,②
①+②得2(a12+a10+a8+a6+a4+a2+a0)=730.
故a12+a10+a8+a6+a4+a2+a0=365.
点评:在解数学题时,将问题中的某些元素用适当的数表示,再进行运算、推理解题的方法叫赋值法,用赋值法解题有两种类型:(1)常规数学问题中,恰当地对字母取值,简化解题过程;(2)非常规数学问题通过赋值,把问题“数学化”.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
已知a,b,c均为整数,且满足a2+b2+c2+3<ab+3b+2c.则以a+b,c-b为根的一元二次方程是( )
| A、x2-3x+2=0 |
| B、x2+2x-8=0 |
| C、x2-4x-5=0 |
| D、x2-2x-3=0 |
已知关于x的二次方程2x2+ax-2a+1=0的两个实数根的平方和是7
,则a的值为( )
| 1 |
| 4 |
| A、11或3 | B、11 | C、3 | D、5 |
 航导弹.
航导弹.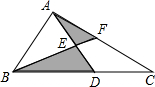 如图,△ABC的面积等于25cm2,AE=ED,BD=2DC.则△AEF与△BDE的面积之和等于
如图,△ABC的面积等于25cm2,AE=ED,BD=2DC.则△AEF与△BDE的面积之和等于 《时代数学学习》杂志2007年3月将改版为《时代学习报•数学周刊》,其徽标是我国古代“弦图”的变形(见示意图).该图可由直角三角形ABC绕点O同向连续旋转三次(每次旋转90°)而得.因此有“数学风车”的动感.假设中间小正方形的面积为1,整个徽标(含中间小正方形)的面积为92,AD=2,则徽标的外围周长为
《时代数学学习》杂志2007年3月将改版为《时代学习报•数学周刊》,其徽标是我国古代“弦图”的变形(见示意图).该图可由直角三角形ABC绕点O同向连续旋转三次(每次旋转90°)而得.因此有“数学风车”的动感.假设中间小正方形的面积为1,整个徽标(含中间小正方形)的面积为92,AD=2,则徽标的外围周长为