题目内容
你能很快算出19952吗?
为了解决这个问题,我们考察个位上的数字为5的自然数的平方,任意一个个位数为5的自然数可写成10n+5(n为自然数),即求(10n+5)2的值,试分析n=1,n=2,n=3…这些简单情形,从中探索其规律,并归纳猜想出结论.
(1)通过计算,探索规律.
152=225可写成100×1×(1+1)+25;252=625可写成100×2×(2+1)+25;352=1225可写成100×3×(3+1)+25;452=2025可写成100×4×(4+1)+25;…752=5625可写成 ;852=7225可写成 .
(2)从第(1)题的结果,归纳、猜想得(10n+5)2= .
(3)根据上面的归纳猜想,请算出19952= .
为了解决这个问题,我们考察个位上的数字为5的自然数的平方,任意一个个位数为5的自然数可写成10n+5(n为自然数),即求(10n+5)2的值,试分析n=1,n=2,n=3…这些简单情形,从中探索其规律,并归纳猜想出结论.
(1)通过计算,探索规律.
152=225可写成100×1×(1+1)+25;252=625可写成100×2×(2+1)+25;352=1225可写成100×3×(3+1)+25;452=2025可写成100×4×(4+1)+25;…752=5625可写成
(2)从第(1)题的结果,归纳、猜想得(10n+5)2=
(3)根据上面的归纳猜想,请算出19952=
考点:完全平方公式
专题:规律型
分析:认真阅读,总结规律:100×十位数×(十位数+1)+25,然后按规律答题.
解答:解:(1)752=5625=100×7×(7+1)+25;852=7225=100×8×(8+1)+25;
(2)(10n+5)2=100n(n+1)+25.
(3)19952=100×199×(199+1)+25=3980000+25=3980025.
故答案为:3980025.
(2)(10n+5)2=100n(n+1)+25.
(3)19952=100×199×(199+1)+25=3980000+25=3980025.
故答案为:3980025.
点评:此题结合实际问题考查完全平方公式,解答此题的关键是理清题意,找准规律解题.

练习册系列答案
相关题目
一个四位数具有这样的性质:用它的后两位数去除这个四位数得到一个完全平方数(如果它的十位数字是0,就只用个位数字去除),且这个完全平方数正好是前两位数加1的平方,则具有上述性质的四位数共有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
如果实数x满足方程:|2-x|=2+|x|,那么|2-x|等于( )
| A、±(x-2) | B、1 |
| C、2-x | D、x-2 |
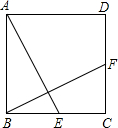 正方形ABCD中,E为BC的中点,F为CD的中点,求证:AE⊥BF.
正方形ABCD中,E为BC的中点,F为CD的中点,求证:AE⊥BF.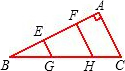 如图,Rt△ABC中,
如图,Rt△ABC中,