题目内容
20.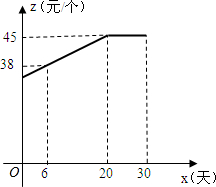 商人陈某打算对现有门面进行转型投资.经过考察,发现其门面所在的融侨公园附近有几所规模不小的学校却没有相应的文具店.为了保证投资利益,陈某决定针对某些常用文具进行调研.该门面在开学前采购了一种今年新上市的文具袋,准备9月份(9月1日至9月30日)进行30天的试销售,购进价格为20元/个.销售结束后,得知日销量y(个)与销售时间x天之间有如下关系:y=-2x+80(1≤x≤30,且x为整数);又知销售价格z(元/个)与销售时间x之间的函数关系满足如图所示的函数图象.
商人陈某打算对现有门面进行转型投资.经过考察,发现其门面所在的融侨公园附近有几所规模不小的学校却没有相应的文具店.为了保证投资利益,陈某决定针对某些常用文具进行调研.该门面在开学前采购了一种今年新上市的文具袋,准备9月份(9月1日至9月30日)进行30天的试销售,购进价格为20元/个.销售结束后,得知日销量y(个)与销售时间x天之间有如下关系:y=-2x+80(1≤x≤30,且x为整数);又知销售价格z(元/个)与销售时间x之间的函数关系满足如图所示的函数图象.(1)求z于x的函数关系式;
(2)在这30天(9月1日至9月30日)的试销中,第x天的日销售利润为1125元,求x.
分析 (1)根据图象得出销售价格z与销售时间x(天)的关系为一次函数关系,进而求出即可;
(2)根据当1≤x≤20时,以及当20<x≤30时,表示出日销售利润,进而求出函数关系式,代入解答即可.
解答 (1)由图象知,当1≤x≤20时,设z=kx+b,
则有:$\left\{\begin{array}{l}{38=6k+b}\\{45=20k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=35}\end{array}\right.$,
即z=$\frac{1}{2}$x+35,
当20<x≤30时z=45,
综上:z=$\left\{\begin{array}{l}{\frac{1}{2}x+35,(1≤x≤20)}\\{45,(20<x≤30)}\end{array}\right.$;
(2)当1≤x≤20时,
W=yz-20y=(-2x+80)( $\frac{1}{2}$x+35)-20(-2x+80),
=-x2+10x+1200
当20<x≤30时,
W=yz-20y=45(-2x+80)-20(-2x+80)
=-50x+2000,
即W=$\left\{\begin{array}{l}{-{x}^{2}+10x+1200,(1≤x≤20)}\\{-50x+2000,(20<x≤30)}\end{array}\right.$
9月30日的价格为45元,日销售量为20个,
9月份当1≤x≤20时日销售利润为:
W=-x2+10x+1200=-(x2-10x+25)+1225=-(x-5)2+1225,
当9月5日时日利润最大为1225元.
当20<x≤30时,利润为W=-50x+2000,
当x增加时W减小,故为x=21时最大.最大日销售利润为950元,
综上9月份日销售利润最大为1225元.
故把W=1125代入W=-(x-5)2+1225中,可得:x=15,
在这30天(9月1日至9月30日)的试销中,第15天的日销售利润为1125元.
点评 此题主要考查了二次函数与一次函数的应用和一元二次方程的应用,根据已知得出利润与销量之间的函数关系式是解题关键.

| A. | 5 | B. | 6 | C. | 25 | D. | 26 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | 方程x2+x-2=0有一根为-1 | |
| B. | 方程x2+x=0有一根为1 | |
| C. | 方程x2+3x-4=0有两个不相等的实数根 | |
| D. | 方程x2+4=0有两个实数根,并且这两根互为相反数 |
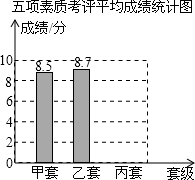 学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为区级先进班集体,下表是这三个班的五项素质考评得分表.五项素质考评得分表(单位:分):
学校通过初评决定最后从甲、乙、丙三个班中推荐一个班为区级先进班集体,下表是这三个班的五项素质考评得分表.五项素质考评得分表(单位:分):| 班级 | 行为规范 | 学习成绩 | 校运动会 | 艺术获奖 | 劳动卫生 |
| 甲班 | 10 | 10 | 6 | 10 | 7 |
| 乙班 | 10 | 8 | 8 | 9 | 8 |
| 丙班 | 9 | 10 | 9 | 6 | 9 |
(1)请你补全五项成绩考评分析表中的数据:五项成绩考评分析表:
| 班级 | 平均分 | 众数 | 中位数 |
| 甲班 | 8.6 | 10 | ③ |
| 乙班 | 8.6 | ② | 8 |
| 丙班 | ① | 9 | 9 |
(3)如果学校把行为规范、学习成绩、校运动会、艺术获奖、劳动卫生五项考评成绩按照3:2:1:1:3的比确定,学生处的李老师根据这个平均成绩,绘制一幅不完整的条形统计图,请将这个统计图补充完整,依照这个成绩,应推荐哪个班为区级先进班集体?
 如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.请你画出以下图形:
如图,在10×10正方形网格中,每个小正方形的边长均为1个单位.请你画出以下图形: