题目内容
已知:如图1,在△ABC中,∠ABC、∠ACB的角平分线交于点O,∠ABC、∠ACB的外角平分线交于点D.
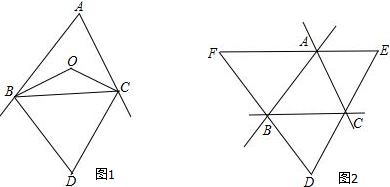
(1)求证:∠BOC+∠BDC=180°;
(2)若△ABC的三个外角平分线交点为D、E、F(如图2),求证:△DEF为锐角三角形.

(1)求证:∠BOC+∠BDC=180°;
(2)若△ABC的三个外角平分线交点为D、E、F(如图2),求证:△DEF为锐角三角形.
考点:三角形内角和定理,三角形的外角性质,多边形内角与外角
专题:证明题
分析:(1)如图1,根据角平分线的定义得到∠1=
∠ABC,∠3=
∠CBE,则利用平角的定义得到∠1+∠3=90°,同理可得∠2+∠4=90°,然后根据四边形的内角和即可得到∠BOC+∠BDC=180°;
(2)如图2,根据角平分线定义得∠1=∠2,∠3=∠4,再利用三角形外角性质得∠1+∠2=∠BAC+∠ACB=∠BAC+180°-∠3-∠4,则∠1+∠3=90°+
∠BAC,然后根据三角形内角和定理得到∠D=180°-(∠1+∠3)=90°-
∠BAC,于是可判断∠D为锐角,同理可得∠F=90°-
∠ACB,∠E=90°-
∠ABC,也可判断∠E、∠F都是锐角,所以△DEF为锐角三角形.
| 1 |
| 2 |
| 1 |
| 2 |
(2)如图2,根据角平分线定义得∠1=∠2,∠3=∠4,再利用三角形外角性质得∠1+∠2=∠BAC+∠ACB=∠BAC+180°-∠3-∠4,则∠1+∠3=90°+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:证明:(1)如图1,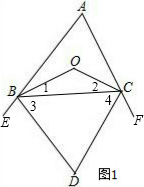
∵OB平分∠ABC,
∴∠1=
∠ABC,
∵BD平分∠CBE,
∴∠3=
∠CBE,
∵∠ABC+∠CBE=180°,
∴∠1+∠3=
×180°=90°,
同理可得∠2+∠4=90°,
在四边形OBDC中,
∵∠OBD+∠BOC+∠OCD+∠BDC=360°,
∴∠BOC+∠BDC=180°;
(2) 如图2,
如图2,
∵BD和CD为△ABC的外角平分线,
∴∠1=∠2,∠3=∠4,
∵∠1+∠2=∠BAC+∠ACB
=∠BAC+180°-∠3-∠4,
∴2∠1=∠BAC+180°-2∠3,
∴∠1+∠3=90°+
∠BAC,
∴∠D=180°-(∠1+∠3)=90°-
∠BAC,
∴∠D为锐角,
同理可得∠F=90°-
∠ACB,∠E=90°-
∠ABC,
∴∠E、∠F都是锐角,
∴△DEF为锐角三角形.

∵OB平分∠ABC,
∴∠1=
| 1 |
| 2 |
∵BD平分∠CBE,
∴∠3=
| 1 |
| 2 |
∵∠ABC+∠CBE=180°,
∴∠1+∠3=
| 1 |
| 2 |
同理可得∠2+∠4=90°,
在四边形OBDC中,
∵∠OBD+∠BOC+∠OCD+∠BDC=360°,
∴∠BOC+∠BDC=180°;
(2)
 如图2,
如图2,∵BD和CD为△ABC的外角平分线,
∴∠1=∠2,∠3=∠4,
∵∠1+∠2=∠BAC+∠ACB
=∠BAC+180°-∠3-∠4,
∴2∠1=∠BAC+180°-2∠3,
∴∠1+∠3=90°+
| 1 |
| 2 |
∴∠D=180°-(∠1+∠3)=90°-
| 1 |
| 2 |
∴∠D为锐角,
同理可得∠F=90°-
| 1 |
| 2 |
| 1 |
| 2 |
∴∠E、∠F都是锐角,
∴△DEF为锐角三角形.
点评:本题考查了三角形内角和定理:三角形内角和是180°.也考查了多边形的内角与外角.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
下列用含字母的数字表示的数量关系中,错误的是( )
A、“a与b两数的倒数和“可表示为
| ||||
B、“与m的积是
| ||||
| C、“x的相反数与y的差的2倍“可表示为2(-x-y) | ||||
| D、“比a和b两数差的平方小3的数“可表示为(a2-b2)-3 |
 在圆内接正方形ABCD中,AC是对角线,BE⊥AC于点E,点F为弧CD的中点,链接AF交CD于P,连接DF,则图中相似三角形有
在圆内接正方形ABCD中,AC是对角线,BE⊥AC于点E,点F为弧CD的中点,链接AF交CD于P,连接DF,则图中相似三角形有 如图,△ABC、△ACD是一副斜边相等的直角三角板,连接BD交公共的斜边AC于点O,求∠COD的度数.
如图,△ABC、△ACD是一副斜边相等的直角三角板,连接BD交公共的斜边AC于点O,求∠COD的度数.
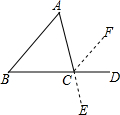 小明在证明“三角形内角和等于180°”时用了如图所示的辅助线的方法,即延长BC到D,延长AC到E,过点C作CF∥AB,你能接着他的辅助线的作法证明出来吗?
小明在证明“三角形内角和等于180°”时用了如图所示的辅助线的方法,即延长BC到D,延长AC到E,过点C作CF∥AB,你能接着他的辅助线的作法证明出来吗?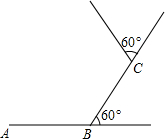 如图,小东在足球场的中间位置,从A点出发,每走6m向左转60°,已知AB=BC=6m.
如图,小东在足球场的中间位置,从A点出发,每走6m向左转60°,已知AB=BC=6m.