题目内容
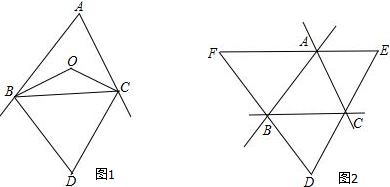
 在圆内接正方形ABCD中,AC是对角线,BE⊥AC于点E,点F为弧CD的中点,链接AF交CD于P,连接DF,则图中相似三角形有
在圆内接正方形ABCD中,AC是对角线,BE⊥AC于点E,点F为弧CD的中点,链接AF交CD于P,连接DF,则图中相似三角形有考点:相似三角形的判定
专题:
分析:根据正方形的性质易得△ABC、△ADC、△ABE和△BCE都是等腰直角三角形,则根据相似三角形的判定方法得到△ABC∽△ADC∽△AEB∽△BEC;再利用点F为弧CD的中点得到
=
,则根据圆周角得到得到∠DAF=∠CAF=∠CDF,∠ACD=∠F,于是根据相似三角形的判定即可得到△ACP∽△AFE∽DPF,然后数出相似三角形的对数即可.
 |
| DF |
 |
| CF |
解答:解:∵四边形为圆内接正方形ABCD,
∴△ABC和△ADC都是等腰直角三角形,
∵BE⊥AC,
∴△ABE和△BCE都是等腰直角三角形,
∴△ABC∽△ADC∽△AEB∽△BEC;
∵点F为弧CD的中点,
∴
=
,
∴∠DAF=∠CAF=∠CDF,
∵∠ACD=∠F,
∴△ACP∽△AFE∽DPF,
∴图中相似三角形有9对.
故答案为9.
∴△ABC和△ADC都是等腰直角三角形,
∵BE⊥AC,
∴△ABE和△BCE都是等腰直角三角形,
∴△ABC∽△ADC∽△AEB∽△BEC;
∵点F为弧CD的中点,
∴
 |
| DF |
 |
| CF |
∴∠DAF=∠CAF=∠CDF,
∵∠ACD=∠F,
∴△ACP∽△AFE∽DPF,
∴图中相似三角形有9对.
故答案为9.
点评:本题考查了相似三角形的判定:有两组角对应相等的两个三角形相似.也考查了正方形的性质、等腰直角三角形的性质和圆周角定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
⊙P的半径为8,圆心P(2,1),点A的坐标为(-6,1),则点A( )
| A、点A在⊙O内 |
| B、点A在⊙O外 |
| C、点A在⊙O上 |
| D、不能确定 |