题目内容
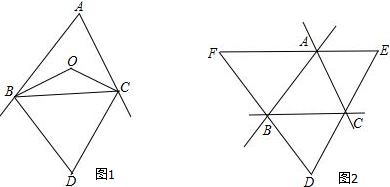
 如图,△ABC、△ACD是一副斜边相等的直角三角板,连接BD交公共的斜边AC于点O,求∠COD的度数.
如图,△ABC、△ACD是一副斜边相等的直角三角板,连接BD交公共的斜边AC于点O,求∠COD的度数.考点:三角形的外角性质
专题:
分析:判断出点A、B、C、D四点共圆,再根据在同圆或等圆中,同弧所对的圆周角相等可得∠CBD=∠CAD,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.
解答:解:∵△ABC、△ACD是一副斜边相等的直角三角板,
∴点A、B、C、D四点共圆,
∴∠CBD=∠CAD=30°,
∴∠COD=∠ACB+∠CBD=45°+30°=75°.
∴点A、B、C、D四点共圆,
∴∠CBD=∠CAD=30°,
∴∠COD=∠ACB+∠CBD=45°+30°=75°.
点评:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质是解题的关键,难点在于利用四点共圆求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
现有若干个三角形,在所有的内角中,有4个直角,2个钝角,21个锐角,则在这些三角形中锐角三角形的个数是( )
| A、15 | B、5 | C、6 | D、3 |
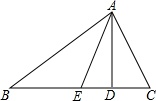 如图AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=70°,求∠AED的度数.
如图AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=70°,求∠AED的度数.