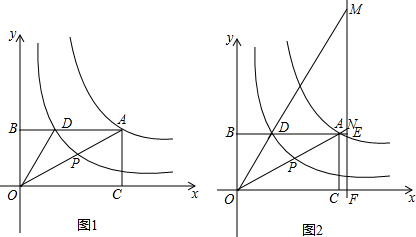
题目内容
如图,矩形ACOB的顶点A坐标为(4a,2a),顶点B、C分别在y轴、x轴上,双曲线l1:y=
(x>0)经过点A,双曲线l2:y=
(x>0)经过OA的中点P,交AB于点D.
(1)填空:双曲线11的表达式是 (用a表示)
(2)求双曲线l2稍微表达式.(用a表示)
操作:在射线BA上取点E,使BE=4,过E作EF⊥x轴,EF与直线OD,OA分别交于点M.N.
(3)如图2,如果0<a<1,
①△BOD与△BAO相似吗?请证明你的结论.
②ME-NE的值是定值吗?如果是,请求出这个定值;如果不是请说明理由.
(4)如果a>4,请直接写出ME与NE之间的数量关系式.
| k |
| x |
| m |
| x |
(1)填空:双曲线11的表达式是
(2)求双曲线l2稍微表达式.(用a表示)
操作:在射线BA上取点E,使BE=4,过E作EF⊥x轴,EF与直线OD,OA分别交于点M.N.
(3)如图2,如果0<a<1,
①△BOD与△BAO相似吗?请证明你的结论.
②ME-NE的值是定值吗?如果是,请求出这个定值;如果不是请说明理由.
(4)如果a>4,请直接写出ME与NE之间的数量关系式.

考点:反比例函数综合题,待定系数法求一次函数解析式,待定系数法求反比例函数解析式,相似三角形的判定
专题:综合题
分析:(1)只需用待定系数法就可解决问题;
(2)只需利用中点坐标公式求出点P的坐标,然后用待定系数法就可解决问题;
(3)①只需用a的代数式表示出BD、OB、BA的长度,然后运用相似三角形的判定(2)就可解决问题;
②可先求出直线OA、直线OD的解析式,然后再求出点M、N的纵坐标,就可解决问题;
(4)由a>4可得点E在线段BD上,然后借鉴(3)②的解题经验,就可解决问题.
(2)只需利用中点坐标公式求出点P的坐标,然后用待定系数法就可解决问题;
(3)①只需用a的代数式表示出BD、OB、BA的长度,然后运用相似三角形的判定(2)就可解决问题;
②可先求出直线OA、直线OD的解析式,然后再求出点M、N的纵坐标,就可解决问题;
(4)由a>4可得点E在线段BD上,然后借鉴(3)②的解题经验,就可解决问题.
解答:解:(1)∵双曲线y=
(x>0)经过点A(4a,2a),
∴k=4a×2a=8a2,
∴双曲线l1的表达式为y=
.
故答案为:y=
.
(2)如图1,

∵点P为OA的中点,A(4a,2a),
∴点P的坐标为(2a,a).
∵双曲线y=
(x>0)经过点P,
∴m=2a×a=2a2,
∴双曲线l2的表达式为y=
.
(3)①△BOD∽△BAO.
证明:由题可得:yD=yA=2a.
∵点D在双曲线y=
上,
∴
=2a,
解得:x=a,
∴点D的坐标为(a,2a),
∴BD=a.
∵四边形ACOB是矩形,A(4a,2a),
∴AB=4a,OB=2a,
∴
=
=
.
∵∠OBD=∠ABO,
∴△BOD∽△BAO.
②ME-NE的值是定值.
由题可得:xM=xN=xE=4.
∵0<a<1,
∴AB=4a<4.
∵BE=4,
∴AB<BE,
∴点E在线段BA的延长线上,如图2.

∵点D(a,2a),
∴直线OD的解析式为y=2x,
∴yM=2×4=8.
∵点A(4a,2a),
∴直线OA的解析式为y=
x,
∴yN=
×4=2,
∴ME-NE=MN=yM-yN=8-2=6.
(4)当a>4时,BD=a>BE,
∴点E在线段BD上,如图3,

同理可得yM=8,yN=2.
∴NE-ME=MN=yM-yN=6.
∴ME与NE之间的数量关系式为NE-ME=6.
| k |
| x |
∴k=4a×2a=8a2,
∴双曲线l1的表达式为y=
| 8a2 |
| x |
故答案为:y=
| 8a2 |
| x |
(2)如图1,

∵点P为OA的中点,A(4a,2a),
∴点P的坐标为(2a,a).
∵双曲线y=
| m |
| x |
∴m=2a×a=2a2,
∴双曲线l2的表达式为y=
| 2a2 |
| x |
(3)①△BOD∽△BAO.
证明:由题可得:yD=yA=2a.
∵点D在双曲线y=
| 2a2 |
| x |
∴
| 2a2 |
| x |
解得:x=a,
∴点D的坐标为(a,2a),
∴BD=a.
∵四边形ACOB是矩形,A(4a,2a),
∴AB=4a,OB=2a,
∴
| BD |
| BO |
| BO |
| BA |
| 1 |
| 2 |
∵∠OBD=∠ABO,
∴△BOD∽△BAO.
②ME-NE的值是定值.
由题可得:xM=xN=xE=4.
∵0<a<1,
∴AB=4a<4.
∵BE=4,
∴AB<BE,
∴点E在线段BA的延长线上,如图2.

∵点D(a,2a),
∴直线OD的解析式为y=2x,
∴yM=2×4=8.
∵点A(4a,2a),
∴直线OA的解析式为y=
| 1 |
| 2 |
∴yN=
| 1 |
| 2 |
∴ME-NE=MN=yM-yN=8-2=6.
(4)当a>4时,BD=a>BE,
∴点E在线段BD上,如图3,

同理可得yM=8,yN=2.
∴NE-ME=MN=yM-yN=6.
∴ME与NE之间的数量关系式为NE-ME=6.
点评:本题主要考查了用待定系数法求反比例函数及一次函数的解析式、相似三角形的判定、矩形的性质等知识,需要注意的是ME与NE的之间的大小关系与a的取值有关.

练习册系列答案
相关题目
下列各组中的四条线段成比例的是( )
| A、4、2、1、3 |
| B、1、2、3、5 |
| C、3、4、5、6 |
| D、1、2、2、4 |
 如图,图中小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形顶点上.
如图,图中小方格都是边长为1的正方形,△ABC与△A′B′C′是关于点O为位似中心的位似图形,它们的顶点都在小正方形顶点上.