题目内容
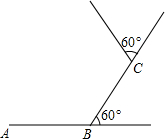 如图,小东在足球场的中间位置,从A点出发,每走6m向左转60°,已知AB=BC=6m.
如图,小东在足球场的中间位置,从A点出发,每走6m向左转60°,已知AB=BC=6m.(1)小东是否能走回A点,若能回到A点,则需走几m,走过的路径是一个什么图形?为什么?(路径A到B到C到…)
(2)求出这个图形的内角和.
考点:多边形内角与外角
专题:应用题
分析:(1)利用外角和为360°计算出多边形的边数即可;
(2)利用内角和公式直接计算即可.
(2)利用内角和公式直接计算即可.
解答:解:(1)∵从A点出发,每走6m向左转60°,
∴360°÷60°=6,
∴走过的路径是一个边长为6的正六边形;
(2)正六边形的内角和为:(6-2)×180°=720°.
∴360°÷60°=6,
∴走过的路径是一个边长为6的正六边形;
(2)正六边形的内角和为:(6-2)×180°=720°.
点评:本题考查了多边形的内角和外角,解题的关键是了解正六边形的内角和和外角和定理,难度不大.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
现有若干个三角形,在所有的内角中,有4个直角,2个钝角,21个锐角,则在这些三角形中锐角三角形的个数是( )
| A、15 | B、5 | C、6 | D、3 |
无论m为何值,一次函数y=(m-1)x-1的图象总是经过点( )
| A、(1,-1) |
| B、(1,0) |
| C、(0,-1) |
| D、(0,1) |

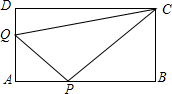 如图,矩形ABCD中AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm╱s的速度移动,点Q沿DA边从点D开始向点A以1cm╱s的速度移动,如果点P,Q同时出发,用t(s)表示移动时间(0≤t≤6).那么:
如图,矩形ABCD中AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm╱s的速度移动,点Q沿DA边从点D开始向点A以1cm╱s的速度移动,如果点P,Q同时出发,用t(s)表示移动时间(0≤t≤6).那么: