题目内容
2.在Rt△ABC中,∠C=90°,AC=5cm,BC=12cm.以C为圆心,r为半径作圆.①当r满足r<$\frac{60}{13}$cm时,直线AB与⊙C相离;
②当r满足r=$\frac{60}{13}$cm时,直线AB与⊙C相切;
③当r满足r>$\frac{60}{13}$cm时,直线AB与⊙C相交;
④当r满足r=$\frac{60}{13}$cm或r=5cm时,线段AB与⊙C只有一个公共点.
分析 根据题意画出图形,过点C作CD⊥AB于点D,由勾股定理求出AB的长,再求出CD的长,根据直线与圆的三种位置关系进行解答即可.
解答 解:过点C作CD⊥AB于点D,
∵Rt△ABC中,∠C=90°,BC=5cm,AC=12cm,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
CD=$\frac{AC•BC}{AB}$=$\frac{12×5}{13}$=$\frac{60}{13}$,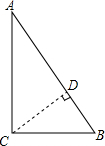
∴①当r<$\frac{60}{13}$cm时,⊙C和直线AB相离;
②当r=$\frac{60}{13}$cm时,⊙C和直线AB相切;
③当r>$\frac{60}{13}$cm时,⊙C和直线AB相交;
④当r=$\frac{60}{13}$cm或r=5cm时,线段AB与⊙C只有一个公共点.
故答案为:r<$\frac{60}{13}$cm,r=$\frac{60}{13}$cm,r>$\frac{60}{13}$cm,r=$\frac{60}{13}$cm或r=5cm.
点评 本题考查的是直线与圆的位置关系,根据题意画出图形,利用勾股定理求出AB的长,再根据直线与圆的位置关系是解答此题的关键.

练习册系列答案
相关题目
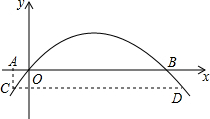 如图是某拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-$\frac{1}{400}$(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴.若OA=10米,则桥面离水面的高度AC为$\frac{17}{4}$米.
如图是某拱形大桥的示意图,桥拱与桥面的交点为O,B,以点O为原点,水平直线OB为x轴,建立平面直角坐标系,桥的拱形可以近似看成抛物线y=-$\frac{1}{400}$(x-80)2+16,桥拱与桥墩AC的交点C恰好在水面,有AC⊥x轴.若OA=10米,则桥面离水面的高度AC为$\frac{17}{4}$米. 已知:如图,BE平分∠ABC,CE平分∠ACD,且交BE于点E.试说明:点E到∠FAC两边的距离相等.
已知:如图,BE平分∠ABC,CE平分∠ACD,且交BE于点E.试说明:点E到∠FAC两边的距离相等.