题目内容
12．
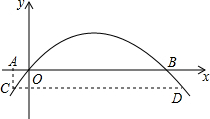如图是某拱形大桥的示意图，桥拱与桥面的交点为O，B，以点O为原点，水平直线OB为x轴，建立平面直角坐标系，桥的拱形可以近似看成抛物线y=-$\frac{1}{400}$（x-80）2+16，桥拱与桥墩AC的交点C恰好在水面，有AC⊥x轴．若OA=10米，则桥面离水面的高度AC为$\frac{17}{4}$米．
分析 先确定C点的横坐标，然后根据抛物线上点的坐标特征求出C点的纵坐标，从而可得到AC的长．
解答 解：∵AC⊥x轴，OA=10米，
∴点C的横坐标为-10，
当x=-10时，y=-$\frac{1}{400}$（x-80）2+16=-$\frac{1}{400}$（-10-80）2+16=-$\frac{17}{4}$，
∴C（-10，-$\frac{17}{4}$），
∴桥面离水面的高度AC为$\frac{17}{4}$m．
故答案为：$\frac{17}{4}$．
点评 本题考查了二次函数的应用：利用二次函数解决抛物线形的隧道、大桥和拱门等实际问题时，要恰当地把这些实际问题中的数据落实到平面直角坐标系中的抛物线上，从而确定抛物线的解析式，通过解析式可解决一些测量问题或其他问题．
练习册系列答案
名题金卷系列答案
优加精卷系列答案
相关题目
2．某项工程由甲队单独做需36天完成，由乙队单独做只需甲队的一半时间完成，设两队合做需x天完成，则可得方程（ ）
| A． | $\frac{1}{36}$+$\frac{1}{18}$=x | B． | （$\frac{1}{36}$+$\frac{1}{18}$）x=1 | C． | $\frac{1}{36}$+$\frac{1}{72}$=x | D． | （$\frac{1}{36}$+$\frac{1}{72}$）x=1 |
在△ABC中，∠A=60°，∠ABC，∠ACB所对的边b，c满足b2+c2-4（b+c）+8=0．
7．将抛物线y=2x2向右平移2个单位，再向上平移3个单位，所得抛物线的表达式为（ ）
| A． | y=2（x+2）2+3 | B． | y=（2x-2）2+3 | C． | y=（2x+2）2-3 | D． | y=2（x-2）2+3 |
17．一次安全知识测验中，学生得分均为整数，满分10分，这次测验中甲、乙两组学生人数都为6人，成绩如下（单位：分）：
甲：7，9，10，8，5，9；
乙：9，6，8，10，7，8
（1）请补充完整下面的成绩统计分析表：
（2）甲组学生说他们的众数高于乙组，所以他们的成绩好于乙组，但乙组学生不同意甲组学生的说法，认为他们组的成绩要好于甲组，请你给出一条支持乙组学生观点的理由．两队平均分相同，但乙的方差小于甲的方差，所以乙的成绩更稳定．
甲：7，9，10，8，5，9；
乙：9，6，8，10，7，8
（1）请补充完整下面的成绩统计分析表：
| 平均分 | 方差 | 众数 | 中位数 | |
| 甲组 | 8 | $\frac{8}{3}$ | 9 | 8.5 |
| 乙组 | 8 | $\frac{5}{3}$ | 8 | 8 |
4．
如图，点A在以O为原点的数轴上，OA的长度为3，以OA为直角边，以长度是1的线段AB为另一直角边作Rt△OAB，若以O为圆心，OB为半径作圆，则圆与数轴交点表示的数为（ ）
如图，点A在以O为原点的数轴上，OA的长度为3，以OA为直角边，以长度是1的线段AB为另一直角边作Rt△OAB，若以O为圆心，OB为半径作圆，则圆与数轴交点表示的数为（ ）| A． | 3.5 | B． | $\sqrt{10}$ | C． | ±2$\sqrt{2}$ | D． | ±$\sqrt{10}$ |
读句画图并回答问题：