题目内容
从地面竖直向上抛射一个物体,在上升过程中,物体向上的速度v(米/秒)是运动时间t(秒)的一次函数.经测量,该物体的初始速度(t=0时物体的速度)为20米/秒,5秒后物体的速度为3米/秒.
(1)写出v与t之间的函数关系式;
(2)经过多长时间,物体将达到最高点?
(1)写出v与t之间的函数关系式;
(2)经过多长时间,物体将达到最高点?
考点:二次函数的应用,一次函数的应用
专题:待定系数法
分析:(1)设v与t之间的函数关系式为y=kx+b,由待定系数法求出将其解就可以得出结论;
(2)根据(1)的一次函数的解析式的性质就可以求出结论.
(2)根据(1)的一次函数的解析式的性质就可以求出结论.
解答:解:(1)设设v与t之间的函数关系式为v=kt+b,由题意,得
,
解得:
,
v与t之间的函数关系式为v=-
t+20.
(2)物体达到最高点,说明物体向上的速度为0,
∴0=-
t+20,
t=
.
答:经过
秒,物体将达到最高点
|
解得:
|
v与t之间的函数关系式为v=-
| 17 |
| 5 |
(2)物体达到最高点,说明物体向上的速度为0,
∴0=-
| 17 |
| 5 |
t=
| 100 |
| 17 |
答:经过
| 100 |
| 17 |
点评:本题考查了待定系数法求一次函数的解析式的运用,一次函数的性质的运用,解答时求出一次函数的解析式是关键.

练习册系列答案
相关题目
 如图,AB、CD为⊙O中两条互相垂直的直径,以点D为圆心,DA为半径作
如图,AB、CD为⊙O中两条互相垂直的直径,以点D为圆心,DA为半径作
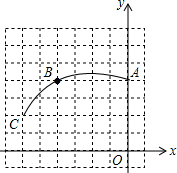 如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作:
如图,在正方形网格图中建立平面直角坐标系,一条圆弧经过网格点A(0,4)、B(-4,4)、C(-6,2),请在网格图中进行如下操作: 如图,已知,△ABC≌△DCB,AC、DB相交于点O,求证:△AOB≌DOC.
如图,已知,△ABC≌△DCB,AC、DB相交于点O,求证:△AOB≌DOC. 已知,如图,点E、F分别为四边形ABCD的对角线AC、BD的中点,求证:EF<
已知,如图,点E、F分别为四边形ABCD的对角线AC、BD的中点,求证:EF<