题目内容
如图，正方形网格中的每个小正方形的边长都是1，每个小格的顶点叫做格点．
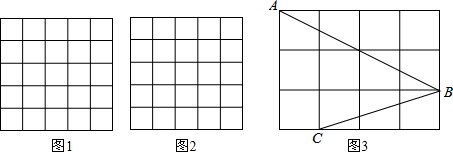
（1）在图1中以格点为顶点画一个面积为10的正方形；
（2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、
、
；
（3）如图3，点A、B、C是小正方形的顶点，求∠ABC的度数．
（1）在图1中以格点为顶点画一个面积为10的正方形；
（2）在图2中以格点为顶点画一个三角形，使三角形三边长分别为2、
| 5 |
| 13 |
（3）如图3，点A、B、C是小正方形的顶点，求∠ABC的度数．
考点：勾股定理
专题：作图题
分析：（1）根据勾股定理画出边长为
的正方形即可；
（2）根据勾股定理和已知画出符合条件的三角形即可；
（3）连接AC、CD，求出△ACB是等腰直角三角形即可．
| 10 |
（2）根据勾股定理和已知画出符合条件的三角形即可；
（3）连接AC、CD，求出△ACB是等腰直角三角形即可．
解答：
解：（1）如图1的正方形的边长是
，面积是10；
（2）如图2的三角形的边长分别为2，
，
；
（3）如图3，连接AC，CD，
则AD=BD=CD=
=
，
∴∠ACB=90°，
由勾股定理得：AC=BC=
=
，
∴∠ABC=∠BAC=45°．
解：（1）如图1的正方形的边长是
| 10 |
（2）如图2的三角形的边长分别为2，
| 5 |
| 13 |
（3）如图3，连接AC，CD，
则AD=BD=CD=
| 22+12 |
| 5 |
∴∠ACB=90°，
由勾股定理得：AC=BC=
| 32+12 |
| 10 |
∴∠ABC=∠BAC=45°．
点评：本题考查了勾股定理，三角形的面积，直角三角形的判定的应用，主要考查学生的计算能力和动手操作能力．
练习册系列答案
相关题目
如图所示，在平行四边形ABCD中，P是AC上任意一点．求证：S△APD=S△APB．请找出下列命题是正确的命题．
①若∠1+∠2=90°，则与∠2互为余角；
②若∠A+∠B=180°，则∠A与互为邻补角；
④同角的余角相等；
⑤由两条射线组成的图形叫做角．
③120°的角和60°的角都是补角．
①若∠1+∠2=90°，则与∠2互为余角；
②若∠A+∠B=180°，则∠A与互为邻补角；
④同角的余角相等；
⑤由两条射线组成的图形叫做角．
③120°的角和60°的角都是补角．
