题目内容
15．
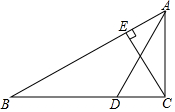如图所示，在△ABC中，AD是∠BAC的平分线交BC于点D，CE是AB边上的高，若∠B=30°，∠BDA=130°，求∠ACE与∠ACB的度数．
分析 根据已知条件得到∠BAD=180°-∠B-∠BDA=20°，根据角平分线的定义得到∠BAC=2∠BAD=40°，根据三角形的内角和即可得到结论．
解答 解：∵∠B=30°，∠BDA=130°，
∴∠BAD=180°-∠B-∠BDA=20°，
∵AD是∠BAC的平分线，
∴∠BAC=2∠BAD=40°，
∴∠ACB=110°，
∵CE是AB边上的高，
∴∠ACE=90°-∠BAC=50°．
点评 本题考查了三角形的内角和，角平分线的性质，熟练掌握三角形的内角和是解题的关键．
练习册系列答案
相关题目
4．袋子中有红球5个，白球6个，则从袋子中摸出白球的概率为（ ）
| A． | $\frac{5}{6}$ | B． | $\frac{6}{11}$ | C． | $\frac{5}{11}$ | D． | $\frac{6}{5}$ |