题目内容
20.解不等式组$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1}\\{1+x<8+3(x-1)}\end{array}\right.$.分析 首先分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集.
解答 解:$\left\{\begin{array}{l}{\frac{x-3}{2}+3≥x+1①}\\{1+x<8+3(x-1)②}\end{array}\right.$,
由①得:x≤1,
由②得:x>-2,
不等式组的解集为:-2<x≤1.
点评 此题主要考查了解一元一次不等式组,关键是掌握解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
9.下列计算错误的是( )
| A. | $\sqrt{\frac{4}{3}}$÷$\sqrt{\frac{1}{21}}$=2$\sqrt{7}$ | B. | ($\sqrt{8}$+$\sqrt{3}$)×$\sqrt{3}$=2$\sqrt{6}$+3 | C. | (4$\sqrt{2}$-3$\sqrt{6}$)÷2$\sqrt{2}$=2-$\frac{3}{2}$$\sqrt{3}$ | D. | ($\sqrt{5}$+7)($\sqrt{5}$-7)=-2 |
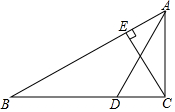 如图所示,在△ABC中,AD是∠BAC的平分线交BC于点D,CE是AB边上的高,若∠B=30°,∠BDA=130°,求∠ACE与∠ACB的度数.
如图所示,在△ABC中,AD是∠BAC的平分线交BC于点D,CE是AB边上的高,若∠B=30°,∠BDA=130°,求∠ACE与∠ACB的度数. 我们学过用直尺和三角尺画平行线的方法,如图所示,直线a∥b的根据是同位角相等,两直线平行.
我们学过用直尺和三角尺画平行线的方法,如图所示,直线a∥b的根据是同位角相等,两直线平行.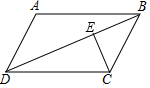 如图,在平行四边形ABCD中,对角线BD=14cm,CE⊥BD,垂足为点E,且CE=5cm,AD=7cm,则AD与BC之间的距离为10cm.
如图,在平行四边形ABCD中,对角线BD=14cm,CE⊥BD,垂足为点E,且CE=5cm,AD=7cm,则AD与BC之间的距离为10cm.