题目内容
 如图,已知AC=AB,AE=AD,∠1=∠2.求证:∠DBC=∠ECB.
如图,已知AC=AB,AE=AD,∠1=∠2.求证:∠DBC=∠ECB.考点:全等三角形的判定与性质
专题:证明题
分析:由已知角相等,利用等式的性质得到夹角相等,利用SAS得到三角形AEC与三角形ADB全等,利用全等三角形对应角相等得到∠3=∠4,再由AB=AC,利用等边对等角得到一对角相等,利用等式的性质变形即可得证.
解答:证明:∵∠1=∠2,
∴∠1+∠BAC=∠2+∠BAC,即∠EAC=∠DAB,
在△AEC和△DAB中,
,
∴△AEC≌△DAB(SAS),
∴∠3=∠4,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC-∠4=∠ACB-∠3,
则∠DBC=∠ECB.
∴∠1+∠BAC=∠2+∠BAC,即∠EAC=∠DAB,
在△AEC和△DAB中,
|
∴△AEC≌△DAB(SAS),
∴∠3=∠4,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABC-∠4=∠ACB-∠3,
则∠DBC=∠ECB.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
当a是不小于
的值时,则5-3a的值( )
| 5 |
| 3 |
| A、小于零 | B、大于零 |
| C、不小于零 | D、不大于零 |
对于一元二次方程x2-bx+c=0,下面的结论错误的是( )
| A、若c=0,则方程必有一根为0 |
| B、若c<0,则方程必有一正数根和一负数根 |
| C、若c>0,b<0,则方程必有两个正数根 |
| D、若b>c+1,则方程一个根大于-1、一个根小于-1 |
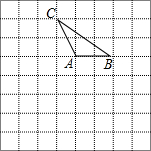 如图,在正方形组成的网格中,△ABC的三个顶点在格点上,现以△ABC的一边再作一个三角形,使所得的三角形与△ABC全等,且其顶点也在格点上,则这样的三角形有
如图,在正方形组成的网格中,△ABC的三个顶点在格点上,现以△ABC的一边再作一个三角形,使所得的三角形与△ABC全等,且其顶点也在格点上,则这样的三角形有