题目内容
18.已知⊙O的半径是2,弦AB,AC的长分别为2$\sqrt{2}$和2$\sqrt{3}$,则∠BAC=15°或75°.分析 根据圆心在∠BAC内部或外部两种情况进行讨论,作出弦心距,根据垂径定理和锐角三角函数解答即可.
解答 解:(1)如图,作OE⊥AB于E,OF⊥AC于F,
则AE=$\frac{1}{2}$AB=$\sqrt{2}$,AF=$\frac{1}{2}$AC=$\sqrt{3}$,
在Rt△AOE中,AE=$\sqrt{2}$,OA=2,
∠OAE=45°,
在Rt△AOF中,AF=$\sqrt{2}$,OA=2,
∠OAF=30°,
∴∠BAC=75°.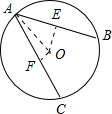
(2)如下图,根据(1)的作法可知,
∠BAC=15°.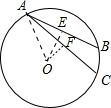
故答案为:15°或75°.
点评 本题考查的是垂径定理和锐角三角函数的应用,正确作出辅助线构造直角三角形是解题的关键,注意分类讨论思想的运用.

练习册系列答案
相关题目
13.直线y=2x-2与x轴交于点A,与y轴交于点B,过点B作直线BP交x轴于点P,且OP=2OA,则△ABP的面积是( )
| A. | 1 | B. | 2 | C. | 1或3 | D. | 2或4 |
7.已知在四边形ABCD中,AB∥CD,添加下列一个条件后,一定能判定四边形ABCD是平行四边形的是( )
| A. | AD=BC | B. | AC=BD | C. | ∠A=∠C | D. | ∠A=∠B |
 二次函数的图象如图所示,则其解析式为y=-x2+2x+3.
二次函数的图象如图所示,则其解析式为y=-x2+2x+3.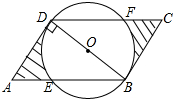 如图,平行四边形ABCD中,AB=6,AD=3,BD⊥AD,以BD为直径的圆交AB于E,交DC于F,则阴影部分的面积$\frac{45\sqrt{3}}{8}$-$\frac{9π}{4}$.
如图,平行四边形ABCD中,AB=6,AD=3,BD⊥AD,以BD为直径的圆交AB于E,交DC于F,则阴影部分的面积$\frac{45\sqrt{3}}{8}$-$\frac{9π}{4}$.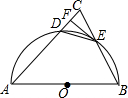 如图,在△ABC中,AB=AC,以AB为直径的半圆O与AC交于点D,与BC交于点E,连接DE,过点E作EF⊥AC,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径的半圆O与AC交于点D,与BC交于点E,连接DE,过点E作EF⊥AC,垂足为点F.