题目内容
20.已知:如图1,已知AB∥DC,∠A=∠C.(1)求证:AD∥BC;
(2)如图2,过B点作BF⊥BC于B,BF交CA的延长线于F,若∠BAF=105°,∠D=2∠ACB,求∠FBA的度数.(说明:不能直接使用三角形内角和定理)
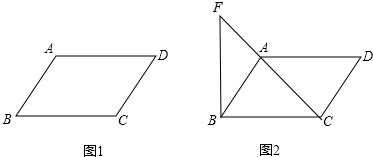
分析 (1)由平行线的性质及判定即可得;
(2)由平行四边形的性质知∠ABC=∠D,由∠D=2∠ACB、∠BAF=105°可得∠ABC=70°,根据BF⊥BC可得∠FBA的度数.
解答 解:(1)∵AB∥DC,
∴∠B+∠C=180°,
又∵∠A=∠C,
∴∠A+∠B=180°,
∴AD∥BC.
(2)∵四边形ABCD是平行四边形,
∴∠ABC=∠D,
又∵∠D=2∠ACB,
∴∠ABC=2∠ACB,即∠ACB=$\frac{1}{2}$∠ABC,
∵∠BAF=∠ABC+∠ACB=105°,
∴∠BAF=$\frac{3}{2}$∠ABC,
∴∠ABC=70°,
∵BF⊥BC,
∴∠FBA=20°.
点评 本题主要考查平行线的判定与性质及平行四边形的性质,熟练掌握平行四边形的性质是解题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
10.为了大力宣传节约用电,某小区随机抽查了10户家庭的月用电量情况,统计如下表,关于这10户家庭的月用电量说法正确的是( )
| 月用电量(度) | 25 | 30 | 40 | 50 | 60 |
| 户数 | 1 | 2 | 4 | 2 | 1 |
| A. | 平均数是20.5 | B. | 众数是4 | ||
| C. | 中位数是40 | D. | 这10户家庭月用电量共205度 |
12.在Rt△ABC中,∠C=90°,a=5,c=13,则b的长为( )
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
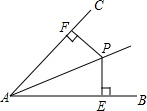 如图,点P是∠BAC的角平分线上的一点,若PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE=PF.理由是角平分线上的点到角的两边的距离相等.
如图,点P是∠BAC的角平分线上的一点,若PE⊥AB,PF⊥AC,垂足分别为点E、F,则PE=PF.理由是角平分线上的点到角的两边的距离相等.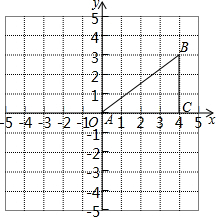 如图,坐标网格中的每个正方形的边长都是1,每个小正方形的顶点叫做格点,△ABC的三个顶点A,B,C都在格点上,点A是坐标原点,AC在x轴的正半轴上.
如图,坐标网格中的每个正方形的边长都是1,每个小正方形的顶点叫做格点,△ABC的三个顶点A,B,C都在格点上,点A是坐标原点,AC在x轴的正半轴上.