题目内容
6.计算:$\frac{{x}^{3}+5{x}^{2}+8x+4}{{x}^{2}+3x+2}$+$\frac{2{x}^{3}+13{x}^{2}+27x+18}{{x}^{2}+5x+6}$-$\frac{3{x}^{3}+26{x}^{2}+71x+59}{{x}^{2}+7x+12}$.
分析 对所求式子进行因式分解,然后约分即可解答本题.
解答 解:$\frac{{x}^{3}+5{x}^{2}+8x+4}{{x}^{2}+3x+2}$+$\frac{2{x}^{3}+13{x}^{2}+27x+18}{{x}^{2}+5x+6}$-$\frac{3{x}^{3}+26{x}^{2}+71x+59}{{x}^{2}+7x+12}$
=$\frac{(x+2)({x}^{2}+3x+2)}{{x}^{2}+3x+2}$+$\frac{(2x+3)({x}^{2}+5x+6)}{{x}^{2}+5x+6}$-$\frac{(3x+5)({x}^{2}+7x+12)}{{x}^{2}+7x+12}$+$\frac{1}{{x}^{2}+7x+12}$
=x+2+2x+3-3x-5+$\frac{1}{{x}^{2}+7x+12}$
=$\frac{1}{{x}^{2}+7x+12}$.
点评 本题考查分式的加减法,解题的关键是可以对题目中的式子因式分解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.下列计算正确的是( )
| A. | 4a-9a=5a | B. | a-a=a | C. | 4a+a=5 | D. | a+a=2a |

 如图所示,已知△ABC中,AD是∠BAC的平分线,E为AD上一点,EF⊥BC于F,∠B=40°,∠C=70°,则∠DEF=15°.
如图所示,已知△ABC中,AD是∠BAC的平分线,E为AD上一点,EF⊥BC于F,∠B=40°,∠C=70°,则∠DEF=15°.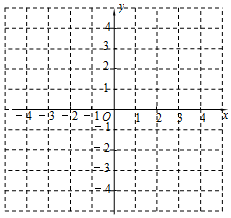 已知一次函数y=kx+b的图象经过点(1,2),(0,4).
已知一次函数y=kx+b的图象经过点(1,2),(0,4).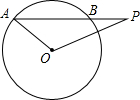 如图,已知⊙O的半径为5cm,弦AB长为8cm,P是AB延长线上一点,BP=2cm,则OP=3$\sqrt{5}$cm.
如图,已知⊙O的半径为5cm,弦AB长为8cm,P是AB延长线上一点,BP=2cm,则OP=3$\sqrt{5}$cm. 如图,已知以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为弧BE的中点,连接AD交OE于点F,若AC=FC
如图,已知以△ABC的BC边上一点O为圆心的圆,经过A,B两点,且与BC边交于点E,D为弧BE的中点,连接AD交OE于点F,若AC=FC