题目内容
9.某商场出售一批进价为2元的贺卡,在营运中发现此商品的日销价为x(元)与销售量y(张)之间有如下关系| x元 | 3 | 4 | 5 | 6 |
| y元 | 20 | 15 | 12 | 10 |
(2)当日销售单价为10元时,贺卡的日销售量是多少张?
(3)设此卡的利润为W元,试求出W与x之间的函数关系式,若物价部门规定此卡的销售单价不能超过10元,试求出当日销售单价为多少元时,每天获得的利润最大并求出最大的利润.
分析 (1)要确定y与x之间的函数关系式,通过观察表中数据,可以发现x与y的乘积是相同的,都是60,所以可知y与x成反比例,用待定系数法求解即可;
(2)代入x=10求得y的值即可;
(3)首先要知道纯利润=(销售单价x-2)×日销售数量y,这样就可以确定w与x的函数关系式,然后根据题目的售价最高不超过10元/张,就可以求出获得最大日销售利润时的日销售单价x.
解答 解:(1)设y=$\frac{k}{x}$(k为常数且k≠0),把点(3,20)代入得,k=60,
所以y=$\frac{60}{x}$;
(2)当x=10时,y=$\frac{60}{10}$=6,
所以日销售单价为10元时,贺卡的日销售量是6张;
(3)∵W=(x-2)y=60-$\frac{120}{x}$,
又∵x≤10,
∴当x=10,W最大,为60-$\frac{120}{10}$=48.
点评 本题考查了反比例函数的定义,两个变量的积是定值,也考查了根据实际问题和反比例函数的关系式求最大值,属于中等难度的题,解答此类题目的关键是仔细理解题意.

练习册系列答案
相关题目
4.若分式$\frac{x-2y}{x+y}$中的x、y的值都变为原来的3倍,则此分式的值( )
| A. | 是原来的3倍 | B. | 不变 | C. | 是原来的$\frac{1}{3}$ | D. | 不能确定 |
19.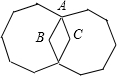 如图,平面上有两个全等的正八边形,∠BAC为( )
如图,平面上有两个全等的正八边形,∠BAC为( )
 如图,平面上有两个全等的正八边形,∠BAC为( )
如图,平面上有两个全等的正八边形,∠BAC为( )| A. | 60° | B. | 45° | C. | 30° | D. | 72° |
