题目内容
17.(1)$\sqrt{3{a}^{2}}$÷$\sqrt{\frac{a}{6}}$(2)($\sqrt{24}$+$\sqrt{0.5}$)-($\sqrt{\frac{1}{8}}$-$\sqrt{6}$)
(3)($\sqrt{7}$+$\sqrt{5}$)($\sqrt{7}$-$\sqrt{5}$)-($\sqrt{3}$+3$\sqrt{2}$)2.
分析 (1)根据二次根式的除法法则运算;
(2)先把各二次根式化为最简二次根式,然后合并即可;
(3)利用平方差公式和完全平方公式计算.
解答 解:(1)原式=$\sqrt{3{a}^{2}•\frac{6}{a}}$
=3$\sqrt{2a}$;
(2)原式=2$\sqrt{6}$+$\frac{\sqrt{2}}{2}$-$\frac{\sqrt{2}}{4}$+$\sqrt{6}$
=3$\sqrt{6}$+$\frac{\sqrt{2}}{4}$;
(3)原式=7-5-(3+6$\sqrt{6}$+18)
=2-21-6$\sqrt{6}$
=-19-6$\sqrt{6}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
8.下列计算正确的是( )
| A. | (-x-y)2=-x2-2xy-y2 | B. | (4x+1)2=16x2+8x+1 | ||
| C. | (2x-3)2=4x2+12x-9 | D. | (a+2b)2=a2+2ab+4b2 |
12.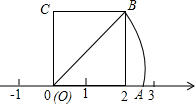 如图,正方形OABC的边长为2,OA在数轴上,以原点为圆心,对角线OB的长为半径画弧,交正半轴于一点D,则点D表示的实数是( )
如图,正方形OABC的边长为2,OA在数轴上,以原点为圆心,对角线OB的长为半径画弧,交正半轴于一点D,则点D表示的实数是( )
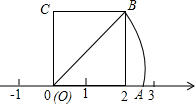 如图,正方形OABC的边长为2,OA在数轴上,以原点为圆心,对角线OB的长为半径画弧,交正半轴于一点D,则点D表示的实数是( )
如图,正方形OABC的边长为2,OA在数轴上,以原点为圆心,对角线OB的长为半径画弧,交正半轴于一点D,则点D表示的实数是( )| A. | 2.5 | B. | 2$\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
9.某商场出售一批进价为2元的贺卡,在营运中发现此商品的日销价为x(元)与销售量y(张)之间有如下关系
(1)猜测并确定y与x的函数关系式;
(2)当日销售单价为10元时,贺卡的日销售量是多少张?
(3)设此卡的利润为W元,试求出W与x之间的函数关系式,若物价部门规定此卡的销售单价不能超过10元,试求出当日销售单价为多少元时,每天获得的利润最大并求出最大的利润.
| x元 | 3 | 4 | 5 | 6 |
| y元 | 20 | 15 | 12 | 10 |
(2)当日销售单价为10元时,贺卡的日销售量是多少张?
(3)设此卡的利润为W元,试求出W与x之间的函数关系式,若物价部门规定此卡的销售单价不能超过10元,试求出当日销售单价为多少元时,每天获得的利润最大并求出最大的利润.
7.下列各数中,最小的是( )
| A. | 0 | B. | 1 | C. | -$\sqrt{3}$ | D. | -$\sqrt{2}$ |