题目内容
16．
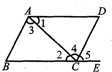如图，下列条件中：（1）∠B+∠BCD=180°；
（2）∠1=∠2；
（3）∠3=∠4；
（4）∠B=∠5．
其中能判定AB∥CD的条件个数有（ ）
| A． | 4 | B． | 3 | C． | 2 | D． | 1 |
分析 根据平行线的判定方法对四个条件分别进行判断即可．
解答 解：（1）∵∠B+∠BCD=180°，∴AB∥CD；
（2）∵∠1=∠2，∴AD∥BC；
（3）∵∠3=∠4，∴AB∥CD；
（4）∵∠B=∠5，∴AB∥CD．
故选B．
点评 本题考查了平行线判定：同位角相等，两直线平行；同旁内角互补，两直线平行；内错角相等，两直线平行．
练习册系列答案
学而优暑期衔接南京大学出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
11．
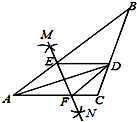如图，在△ABC中，AD平分∠BAC，按如下步骤作图：第一步，分别以点A、D为圆心，以大于AD的一半长为半径在AD两侧作弧，交于两点M、N；第二步，连接MN分别交AB、AC于点E、F；第三步，连接DE、DF，则可以得到四边形AEDF的形状（ ）
如图，在△ABC中，AD平分∠BAC，按如下步骤作图：第一步，分别以点A、D为圆心，以大于AD的一半长为半径在AD两侧作弧，交于两点M、N；第二步，连接MN分别交AB、AC于点E、F；第三步，连接DE、DF，则可以得到四边形AEDF的形状（ ）| A． | 仅仅只是平行四边形 | B． | 是矩形 | ||
| C． | 是菱形 | D． | 无法判断 |
5．下列选项中正确的是（ ）
| A． | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B． | $\frac{2x{y}^{2}}{4{x}^{2}y}$=$\frac{1}{2}$ | C． | $\frac{n}{m}$=$\frac{n-a}{m-a}$ | D． | 若a＞0，则$\sqrt{a^2}=a$ |