题目内容
8.如图,在长方形ABCD中,AB=12厘米,BC=6厘米,点P沿AB边从点A开始向点B以2cm/s的速度移动;点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发,用t(秒)表示移动的时间,那么:(1)如图1,当t为何值时,△QAB的面积等于长方形面积的$\frac{1}{4}$?
(2)如图2,当t为何值时,△QAP为等腰直角三角形?
(3)如图3,P、Q到达B、A后继续运动,P点到达C点后都停止运动.那么当t为何值时,线段AQ的长等于线段CP的长的一半.
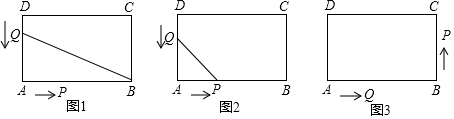
分析 (1)根据已知条件得到DQ=tcm,AQ=(6-t)cm,根据三角形的面积列方程即可得到结论;
(2)根据等腰三角形的性质列方程即可得到结论;
(3)根据已知条件得到AQ=(t-6)cm,CP=(18-2t)cm,依题意使线段AQ的长等于线段CP的长的一半,列方程即可得到结论.
解答 解:(1)由题可知:DQ=tcm,AQ=(6-t)cm,
∵△QAB的面积=$\frac{1}{2}$(6-t)×12,
依题意得:$\frac{1}{2}$(6-t)×12=$\frac{1}{4}$×6×12,
解得:t=3;
(2)由题可知:DQ=tcm,AQ=(6-t)cm,AP=2tcm,
使△QAP为等腰三角形,
∴AQ=AP,
⇒6-t=2t
解得t=2;
(3)由题可知:AQ=(t-6)cm,CP=(18-2t)cm,
依题意使线段AQ的长等于线段CP的长的一半,
∴t-6=$\frac{1}{2}$(18-2t),
解得:t=7.5.
点评 此题考查了动点移动问题,一元一次方程的性质及其应用,三角形的面积的计算,等腰三角形的性质,根据几何图形的边长及面积列方程求出t值是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
7. 如图,点D在△ABC边BC的延长线上,BA=BC,DB=DA,若∠BAC=m,∠ADB=n,则m与n之间的关系是( )
如图,点D在△ABC边BC的延长线上,BA=BC,DB=DA,若∠BAC=m,∠ADB=n,则m与n之间的关系是( )
 如图,点D在△ABC边BC的延长线上,BA=BC,DB=DA,若∠BAC=m,∠ADB=n,则m与n之间的关系是( )
如图,点D在△ABC边BC的延长线上,BA=BC,DB=DA,若∠BAC=m,∠ADB=n,则m与n之间的关系是( )| A. | 3m+n=180° | B. | 4m-n=180° | C. | 3m-n=180° | D. | 2m+n=180° |
8.某中学要推荐一名学生参加全市举办的《我为“金砖”当先锋》的演讲比赛,评委从演讲内容、演讲能力两个方面为选手打分,并分别赋予它们6和4的权.现有甲、乙两位选手进入学校决赛,他们的成绩(百分制)如下表所示:
请计算他们各自的平均成绩,并说明推荐哪位选手参加全市的比赛.
| 选手 | 演讲内容 | 演讲能力 |
| 甲 | 85 | 90 |
| 乙 | 90 | 85 |
5.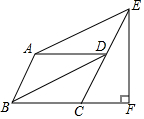 如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
 如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )
如图,在?ABCD中,∠BAD=120°,连接BD,作AE∥BD交CD延长线于点E,过点E作EF⊥BC交BC的延长线于点F,且CF=1,则AB的长是( )| A. | 2 | B. | 1 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
 如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB于D,tan∠B=$\frac{1}{3}$,且BC=9 cm,求AC,AB及CD的长.
如图,在 Rt△ABC中,∠ACB=90°,CD⊥AB于D,tan∠B=$\frac{1}{3}$,且BC=9 cm,求AC,AB及CD的长.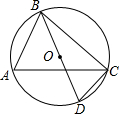 如图,⊙O的直径BD=4,∠A=60°,则CD的长度为2.
如图,⊙O的直径BD=4,∠A=60°,则CD的长度为2. 如图,在?ABCD中,直线EF∥BD,并且与CD、CB的延长线分别交于E、F,交AD于M,交AB于N.求证:EN=FM.
如图,在?ABCD中,直线EF∥BD,并且与CD、CB的延长线分别交于E、F,交AD于M,交AB于N.求证:EN=FM.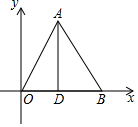 如图,△AOB是等边三角形,B点的坐标为(6,0),AD是高.
如图,△AOB是等边三角形,B点的坐标为(6,0),AD是高.