题目内容
15.在“感恩节”前夕,我市某学生积极参与“关爱孤寡老人”的活动,他们购进一批单价为6元一双的“孝心袜”在课余时间进行义卖,并将所得利润全部捐给乡村孤寡老人,在试卖阶段发现:当销售单价是每双10元时,每天的销售量为200双,销售单价每上涨1元,每天的销售量就减少20双.(1)求销售单价为多少元时,“孝心袜”每天的销售利润最大;
(2)结合上述情况,学生会干部提出了A、B两种营销方案.
方案A:“孝心袜”的销售单价高于进价且不超过11元;
方案B:每天销售量不少于20双,且每双“孝心袜”的利润至少为10元.
请比较哪种方案的最大利润更高,并说明理由.
分析 (1)设销售单价x元,利润为w元.由题意w=(x-6)[200-20(x-10)],利用二次函数的性质即可解决问题.
(2)分别求出两种方案利润的最大值,即可判断.
解答 解:(1)设销售单价x元,利润为w元.
由题意w=(x-6)[200-20(x-10)]=-20(x-13)2+5780.
∵-20<0,
∴x=13时,每天的销售利润最大,
∴销售单价为13元时,“孝心袜”每天的销售利润最大.
(2)方案A:“孝心袜”的销售单价高于进价且不超过11元;
∵w=(x-6)[200-20(x-10)]=-20(x-13)2+5780.
又∵6<x≤11,
∴x=11时,w的值最大,最大值为5740元.
方案B:每天销售量不少于20双,且每双“孝心袜”的利润至少为10元.
∵w=(x-6)[200-20(x-10)]=-20(x-13)2+5780.
又∵16≤x≤19,
∴x=16时,w的值最大,最大值为5600元.
∵5740<5600,
∴方案A的利润最大.
点评 本题考查了二次函数的应用、一元二次方程的应用等知识,最大销售利润的问题常利用函数的增减性来解答,我们首先要吃透题意,确定变量,建立函数模型,然后结合实际选择最优方案.其中要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值不一定在x=$\frac{b}{2a}$时取得.

练习册系列答案
相关题目
6.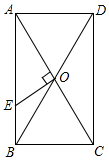 如图,已知矩形ABCD的对角线AC、BD相交于点O,过O点作OE⊥AC,交AB于E,若BC=4,△AOE的面积是5,则下列说法错误的是( )
如图,已知矩形ABCD的对角线AC、BD相交于点O,过O点作OE⊥AC,交AB于E,若BC=4,△AOE的面积是5,则下列说法错误的是( )
 如图,已知矩形ABCD的对角线AC、BD相交于点O,过O点作OE⊥AC,交AB于E,若BC=4,△AOE的面积是5,则下列说法错误的是( )
如图,已知矩形ABCD的对角线AC、BD相交于点O,过O点作OE⊥AC,交AB于E,若BC=4,△AOE的面积是5,则下列说法错误的是( )| A. | AE=5 | B. | ∠BOE=∠BCE | C. | CE⊥OB | D. | sin∠BOE=$\frac{3}{5}$ |
3.下列四组线段中,可以构成直角三角形的是( )
| A. | 1.5,2,3 | B. | 4,5,5 | C. | 2,3,4 | D. | 1,$\sqrt{2}$,1 |
20.已知A、B、C三点在同一直线上,AB=16,BC=10,M、N分别是AB、BC的中点,则MN等于( )
| A. | 2 | B. | 13 | C. | 3或13 | D. | 3 |
5. 如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=60°,则∠C=( )
如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=60°,则∠C=( )
 如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=60°,则∠C=( )
如图,AB是⊙O的直径,CD是⊙O的弦,∠ABD=60°,则∠C=( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |