题目内容
20. 如图,平行四边形ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD.
如图,平行四边形ABCD中,∠ABC=60°,E,F分别在CD和BC的延长线上,AE∥BD.(1)求证:点D为CE中点;
(2)若EF⊥BC,EF=2$\sqrt{3}$,求AB的长.
分析 (1)根据平行四边形性质推出AB=CD,AB∥CD,得出平行四边形ABDE,推出DE=DC=AB,进而可证明点D为CE的中点;
(2)根据直角三角形性质求出CE长,利用勾股定理即可求出AB的长.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四边形ABDE是平行四边形.
∴AB=DE=CD,即D为CE中点.
(2)∵EF⊥BC,
∴∠EFC=90°.
∵AB∥CD,
∴∠DCF=∠ABC=60°.
∴∠CEF=30°.
∵EF=2$\sqrt{3}$,
∴CE=4.
∴AB=CD=DE=2.
点评 本题考查了平行四边形的性质和判定,平行线性质,勾股定理,直角三角形斜边上中线性质,含30度角的直角三角形性质等知识点的应用,此题综合性比较强,是一道比较好的题目.

练习册系列答案
相关题目
11.将a=($\frac{1}{9}$)-1,b=(-10)0,c=(-2)2这三个数按从小到大的顺序排列,为( )
| A. | c<a<b | B. | c<b<a | C. | b<c<a | D. | a<b<c |
10.下列式子中是二元一次方程的是( )
| A. | x+3y=z | B. | 2xy+y=7 | C. | x+y+1 | D. | 2(x+y)=1-x |
 如图,DE∥BC,AD:DB=3:5,则△ADE与△ABC的面积之比为9:64.
如图,DE∥BC,AD:DB=3:5,则△ADE与△ABC的面积之比为9:64.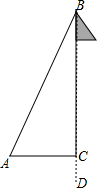 小明想知道学校的旗杆有多高,他发现旗杆顶上的绳子BD垂到地面还多CD=1米,当他把绳子的下端D拉开5米到后,发现下端D刚好接触地面A.你能帮他把旗杆的高度求出来吗?
小明想知道学校的旗杆有多高,他发现旗杆顶上的绳子BD垂到地面还多CD=1米,当他把绳子的下端D拉开5米到后,发现下端D刚好接触地面A.你能帮他把旗杆的高度求出来吗? 如图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5.其中不能判定AB∥CD的条件是( )
如图,有以下四个条件:①∠B+∠BCD=180°,②∠1=∠2,③∠3=∠4,④∠B=∠5.其中不能判定AB∥CD的条件是( ) 如图,AB∥DE,∠1=25°,∠2=110°,求∠BCD的度数.
如图,AB∥DE,∠1=25°,∠2=110°,求∠BCD的度数.