Question

3．函数y=x²+3x+2的图象如图1所示，根据图象回答问题：
（1）当x＜-2或x＞-1时，x²+3x+2＞0；
（2）在上述问题的基础上，探究解决新问题：
①函数y=$\sqrt{（x+1）（x+2）}$的自变量x的取值范围是x≤-2或x≥-1；
②如表是函数y=$\sqrt{（x+1）（x+2）}$的几组y与x的对应值．

x	…	-7	-6	-4	-3	-2	-1	0	1	3	4	…
y	…	5.477…	4.472…	2.449…	1.414…	0	0	1.414…	2.449…	4.472…	5.477…	…

如图2，在平面直角坐标系xOy中，描出了上表中各对对应值为坐标的点的大概位置，请你根据描出的点，画出该函数的图象：
③写出该函数的一条性质：关于直线x=-1.5对称．

Answer 1

分析 （1）当抛物线在x轴上方部分进满足条件，可确定出对应的x的取值范围；
（2）①由二次根式的意义可得到（x+1）（x+2）≥0，可转化为（1）；②利用描点法可画出函数图象；③结合图象可得出答案．

解答 解：
（1）x²+3x+2＞0的解集即抛物线在x轴上方部分对应的自变量的取值范围，
∴x＜-2或x＞-1，
故答案为：＜-2或x＞-1；
（2）①由题意可得（x+1）（x+2）≥0，
由（1）可得x≤-2或x≥-1，
故答案为：x≤-2或x≥-1；
②如图：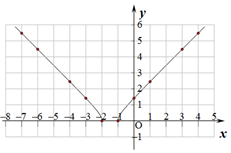

③由图象可知关于直线x=-1.5对称，
故答案为：关于直线x=-1.5对称．

点评 本题主要考查二次函数的性质及函数与方程不等式的关系，利用数形结合是解题的关键．