Question

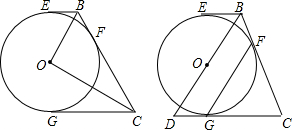
20．在圆心为O的圆外有一点P，设弦AB垂直于直线OP，若直线PA和该圆的交点为C，直线OP和BC相交于点D．求证：OD•OP=OA²．

Answer 1

分析 首先证明∠BOD=∠AMB，∠PCD=∠AMB，接下来证明△OCD∽△OPC即可解决问题．

解答 证明：如图，延长PO交⊙O于M，连接AM、BM、AO、OC、OB．
∵AB⊥OP，
∴$\widehat{AM}$=$\widehat{MB}$，
∴∠AOM=∠BOM，∠AOP=∠POB，
∵∠AOP+∠POB=2∠AMB，
∴∠POB=∠AMB，
∵∠PCD=∠AMB，
∴∠PCD=∠BOD，
∵∠ODB=∠CDP，
∴∠P=∠OBD，
∵OB=OC，
∴∠OCD=∠OBD=∠P，
∵∠COD=∠POC，
∴△OCD∽△OPC，
∴$\frac{OC}{OP}$=$\frac{OD}{OC}$，
∴OC²=OD•OP，
∵OA=OC，
∴OA²=OD•OP．

点评 本题考查圆、相似三角形的判定和性质、垂径定理等知识，解题的关键是添加辅助线构造相似三角形，属于中考常考题型．