题目内容
14.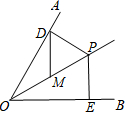 如图,已知OP平分∠AOB,∠AOB=60°,PE=2,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )
如图,已知OP平分∠AOB,∠AOB=60°,PE=2,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据角平分线的性质得到PD=PE=2,根据直角三角形中,30°的直角边是斜边的一半、直角三角形斜边上的中线是斜边的一半得到DM=DP,得到答案.
解答 解:∵OP平分∠AOB,PD⊥OA,PE⊥OB,
∴PD=PE=2,
∵OP平分∠AOB,∠AOB=60°,
∴∠POD=30°,
∵PD⊥OA,
∴PD=$\frac{1}{2}$OP,
∵PD⊥OA,点M是OP的中点,
∴DM=$\frac{1}{2}$OP,
∴DM=DP=2,
故选:B.
点评 本题考查的是角平分线的性质、直角三角形的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目




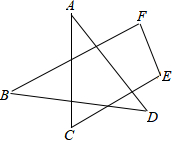 如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
如图,求∠A+∠B+∠C+∠D+∠E+∠F的度数.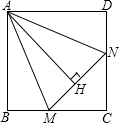 已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M、N,AH⊥MN于点H,如图MH=2,NH=3,求AH的长.
已知,正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB,DC(或它们的延长线)于点M、N,AH⊥MN于点H,如图MH=2,NH=3,求AH的长. 如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使C点与AB边上的点E重合.
如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使C点与AB边上的点E重合.