题目内容
19．
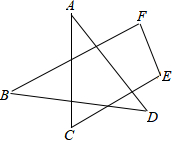如图，求∠A+∠B+∠C+∠D+∠E+∠F的度数．
分析 连接BC，根据三角形的内角和定理即可证得∠A+∠D=∠DBC+∠ACB，则∠A+∠B+∠C+∠D+∠E+∠F=∠DBC+∠ACB+∠DBF+∠ACE+∠E+∠F=∠FBC+∠BCE+∠E+∠F，根据四边形的内角和定理即可求解．
解答 解：连接BC．
∵在△BOC和△AOD中，∠1=∠2，
∴∠A+∠D=∠DBC+∠ACB，
∴∠A+∠B+∠C+∠D+∠E+∠F=∠DBC+∠ACB+∠DBF+∠ACE+∠E+∠F=∠FBC+∠BCE+∠E+∠F=360°．
点评 本题考查了三角形的内角和以及四边形的内角和定理，正确证明∠A+∠D=∠DBC+∠ACB是关键．
练习册系列答案
举一反三同步巧讲精练系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
9．在平面直角坐标系中，如果点P（a，b）到y轴的距离为2，那么（ ）
| A． | a=2 | B． | a=±2 | C． | b=2 | D． | b=±2 |
△ABC与△A′B′C′关于直线l对称，则∠B的度数为105°．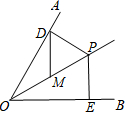
如图，已知OP平分∠AOB，∠AOB=60°，PE=2，PD⊥OA于点D，PE⊥OB于点E．如果点M是OP的中点，则DM的长是（ ）
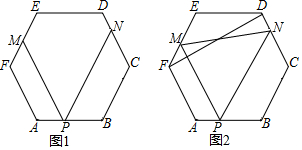在正六边形ABCDEF中，P是AB边上一点，PM∥AF交EF于M，PN∥BC交CD于N．