题目内容
14. 如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使C点与AB边上的点E重合.
如图,一块直角三角形的纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使C点与AB边上的点E重合.(1)求AB的长;
(2)求DE的长.
分析 (1)根据直角三角形的纸片,两直角边AC=6cm,BC=8cm,利用勾股定理即可求出AB;
(2)根据翻折的性质可得AE=AC,DE=CD,∠AED=∠C,设DE=x,表示出BD、BE,然后在R△BDE中,利用勾股定理列方程求解即可.
解答 解:(1)在Rt△ABC中,两直角边AC=6cm,BC=8cm,
∴由勾股定理得,AB=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10(cm);
(2)∵直角边AC沿直线AD折叠落在斜边AB上,且与AE重合,
∴AE=AC=6cm,DE=CD,∠AED=∠C=90°,
设DE=x,则BD=8-x,BE=10-6=4cm,
在Rt△BDE中,由勾股定理得,DE2+BE2=BD2,
即x2+42=(8-x)2,
解得x=3,
即DE=3cm.
点评 本题考查了翻折变换的性质,勾股定理,翻折前后的图形的对应边相等,对应角相等,本题难点在于利用勾股定理列出方程.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
3.下列方程中,没有实数解的是( )
| A. | $\frac{{x}^{2}}{x+2}$=$\frac{4}{x+2}$ | B. | $\sqrt{x-2}$+x=0 | C. | x2-2=0 | D. | x2+y2=1 |
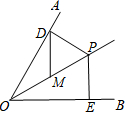 如图,已知OP平分∠AOB,∠AOB=60°,PE=2,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )
如图,已知OP平分∠AOB,∠AOB=60°,PE=2,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )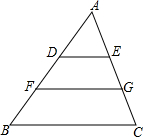 如图,已知△ADE∽△AFG∽△ABC,且△ABC的面积被线段DE、FG三等分,其中BC=12cm,求线段DE和FG的长度.
如图,已知△ADE∽△AFG∽△ABC,且△ABC的面积被线段DE、FG三等分,其中BC=12cm,求线段DE和FG的长度.