题目内容
 如图,矩形ABCD中,AD=2AB,其顶点A、C分别在x轴、y轴正半轴上,点B(6,3)在双曲线y=
如图,矩形ABCD中,AD=2AB,其顶点A、C分别在x轴、y轴正半轴上,点B(6,3)在双曲线y=| k |
| x |
| 8 |
| x |
(1)求k的值;
(2)求OA的长;
(3)以OB、OD为边作平行四边形BODE,判断点E是否在双曲线y=
| k |
| x |
考点:反比例函数综合题
专题:
分析:(1)直接利用反比例函数图象上点的坐标性质求出即可;
(2)首先利用已知得出△ADM∽△BAF,进而得出AF的长,即可得出AO的长;
(3)利用平行四边形的性质进而得出DN以及EN的值即可得出E点坐标,即可得出答案.
(2)首先利用已知得出△ADM∽△BAF,进而得出AF的长,即可得出AO的长;
(3)利用平行四边形的性质进而得出DN以及EN的值即可得出E点坐标,即可得出答案.
解答:
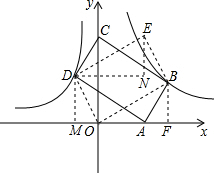 解:(1)∵点B(6,3)在双曲线y=
解:(1)∵点B(6,3)在双曲线y=
(x>0)上,
∴k=6×3=18;
(2)过点B作BF⊥x轴于点F,过点D作DM⊥x轴于点M,
∵矩形ABCD中,∠DAB=90°,
∴∠MAD+∠BAF=90°,
∵∠MDA+∠DAM=90°,
∴∠MDA=∠BAF,
∵∠DMA=∠AFB,
∴△ADM∽△BAF,
∴
=
=
=2,
∵BF=3,OF=6,
∴AM=6,
∴MO=AF,
设AF=x,则MO=x,DM=2x,
故x•2x=|-8|,
解得:x=2,
故AO=6-2=4;
(3)点E不在双曲线y=
(x>0)上.
理由:由(2)可得D点坐标为:(-2,4),
当四边形DOBE是平行四边形,
作DN∥x轴,过点E作EN⊥DN交于点N,
可得DN=FO=6,EN=BF=3,
故E(4,7),
∵4×7=28≠18,
故点E不在双曲线y=
(x>0)上.
 解:(1)∵点B(6,3)在双曲线y=
解:(1)∵点B(6,3)在双曲线y=| k |
| x |
∴k=6×3=18;
(2)过点B作BF⊥x轴于点F,过点D作DM⊥x轴于点M,
∵矩形ABCD中,∠DAB=90°,
∴∠MAD+∠BAF=90°,
∵∠MDA+∠DAM=90°,
∴∠MDA=∠BAF,
∵∠DMA=∠AFB,
∴△ADM∽△BAF,
∴
| AD |
| AB |
| DM |
| AF |
| AM |
| BF |
∵BF=3,OF=6,
∴AM=6,
∴MO=AF,
设AF=x,则MO=x,DM=2x,
故x•2x=|-8|,
解得:x=2,
故AO=6-2=4;
(3)点E不在双曲线y=
| k |
| x |
理由:由(2)可得D点坐标为:(-2,4),
当四边形DOBE是平行四边形,
作DN∥x轴,过点E作EN⊥DN交于点N,
可得DN=FO=6,EN=BF=3,
故E(4,7),
∵4×7=28≠18,
故点E不在双曲线y=
| k |
| x |
点评:此题主要考查了反比例函数图象上点的特征以及平行四边形的性质和相似三角形的判定与性质,得出E点坐标是解题关键.

练习册系列答案
相关题目
关于x的一元二次方程x2-3x+m=0有两个不相等的实数根,则实数m的取值范围是( )
A、m>
| ||
B、m=
| ||
C、m<
| ||
D、m<-
|
甲乙二人都以不变的速度在400米长的环形跑道上跑步,如果同时同地出发,同向而行,则10分钟时乙追上甲;相向而行,则5分钟时甲乙相遇.求甲乙二人跑步的速度.若设甲的速度为x米∕分,乙的速度为y米∕分,则可列方程组( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
 如图是一个用长方形和三角形拼成的图案,
如图是一个用长方形和三角形拼成的图案, 如图,在平面直角坐标系中有等腰直角三角形ABC,A(-2,0),B(0,1),C(-3,2),将△ABC沿x轴正方向平移,在第一象限内,B,C两点的对应点E,F正好落在某反比例函数图象上.
如图,在平面直角坐标系中有等腰直角三角形ABC,A(-2,0),B(0,1),C(-3,2),将△ABC沿x轴正方向平移,在第一象限内,B,C两点的对应点E,F正好落在某反比例函数图象上. 如图,在直角坐标系中,已知坐标轴上两点A(1,0)、B(0,1),P(a,b)是反比例函数y=
如图,在直角坐标系中,已知坐标轴上两点A(1,0)、B(0,1),P(a,b)是反比例函数y=