题目内容
 如图,在直角坐标系中,已知坐标轴上两点A(1,0)、B(0,1),P(a,b)是反比例函数y=
如图,在直角坐标系中,已知坐标轴上两点A(1,0)、B(0,1),P(a,b)是反比例函数y=| 1 |
| 2x |
(1)求线段BE、AF的长(用a,b的代数式表示);
(2)△AOF与△BOE一定相似吗?说明理由;
(3)当P点在曲线上移动时,△OEF的哪个角的大小保持不变,为什么?
考点:反比例函数综合题
专题:
分析:(1))作EH⊥OB于H,作FG⊥OA于G,先证EH∥PD,FG∥PC,得出比例式
=
,
=
,即可求出BE、AF;
(2)先证∠OAB=∠OBA,再证明
=
,即可证出△AOF∽△BOE;
(3)∠EOF=45°保持不变;由△AOF∽△BOE,得出对应角相等∠AFO=∠BOE,再根据外角∠AOF=∠BOF+45°,即可得出结论.
| BE |
| AB |
| EH |
| OA |
| AF |
| AB |
| FG |
| OB |
(2)先证∠OAB=∠OBA,再证明
| AF |
| OA |
| OB |
| BE |
(3)∠EOF=45°保持不变;由△AOF∽△BOE,得出对应角相等∠AFO=∠BOE,再根据外角∠AOF=∠BOF+45°,即可得出结论.
解答:
解:(1)作EH⊥OB于H,作FG⊥OA于G,如图所示:
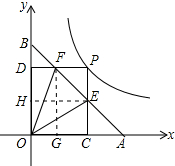 根据题意得:OA=OB=1,EH=a,FG=b,
根据题意得:OA=OB=1,EH=a,FG=b,
∴AB=
,
∵PD⊥OB,PC⊥OA,
∴EH∥PD,FG∥PC,
∴
=
,
=
,
即
=
,
=
,
∴BE=
a,AF=
b;
(2)△AOF∽△BOE;理由如下:
∵P(a,b)是反比例函数y=
的图象在第一象限内的一支上的可动点,
∴ab=
,
∵OA=OB,∠AOB=90°,
∴∠OAB=∠OBA=45°,
∵
=
=
b,
=
=
=
b,
∴
=
,
∴△AOF∽△BOE;
(3)∠EOF=45°保持不变;
∵△AOF∽△BOE,
∴∠AFO=∠BOE,
∵∠AOF=∠BOF+45°,∠BOE=∠EOF+∠BOF,
∴∠EOF=45°.
 根据题意得:OA=OB=1,EH=a,FG=b,
根据题意得:OA=OB=1,EH=a,FG=b,∴AB=
| 2 |
∵PD⊥OB,PC⊥OA,
∴EH∥PD,FG∥PC,
∴
| BE |
| AB |
| EH |
| OA |
| AF |
| AB |
| FG |
| OB |
即
| BE | ||
|
| a |
| 1 |
| AF | ||
|
| b |
| 1 |
∴BE=
| 2 |
| 2 |
(2)△AOF∽△BOE;理由如下:
∵P(a,b)是反比例函数y=
| 1 |
| 2x |
∴ab=
| 1 |
| 2 |
∵OA=OB,∠AOB=90°,
∴∠OAB=∠OBA=45°,
∵
| AF |
| OA |
| ||
| 1 |
| 2 |
| OB |
| BE |
| 1 | ||
|
| ||
| 2a |
| 2 |
∴
| AF |
| OA |
| OB |
| BE |
∴△AOF∽△BOE;
(3)∠EOF=45°保持不变;
∵△AOF∽△BOE,
∴∠AFO=∠BOE,
∵∠AOF=∠BOF+45°,∠BOE=∠EOF+∠BOF,
∴∠EOF=45°.
点评:本题通过反比例函数、相似三角形的判定与性质等知识,考查学生的推理论证和计算能力;证明三角形相似是解题的关键.

练习册系列答案
相关题目
下列说法正确的有( )
| A、4的平方根是2 |
| B、-8没有立方根 |
| C、8的立方根是±2 |
| D、9的算术平方根是3 |
下列说法中不正确的是( )
| A、最小的正整数是1 |
| B、最大的负整数是-1 |
| C、有理数分为正数和负数 |
| D、绝对值最小的有理数是0 |
 如图,正方形ABCD被分成两个小正方形和两个长方形,如果两个小正方形的面积分别是6cm2和2cm2,那么两个长方形的面积和为
如图,正方形ABCD被分成两个小正方形和两个长方形,如果两个小正方形的面积分别是6cm2和2cm2,那么两个长方形的面积和为 如图,矩形ABCD中,AD=2AB,其顶点A、C分别在x轴、y轴正半轴上,点B(6,3)在双曲线y=
如图,矩形ABCD中,AD=2AB,其顶点A、C分别在x轴、y轴正半轴上,点B(6,3)在双曲线y=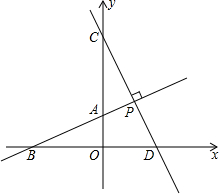 如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA:AC=1:2,D(3,0)直线CD垂直于直线AB于点P,交x轴于点D.
如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA:AC=1:2,D(3,0)直线CD垂直于直线AB于点P,交x轴于点D.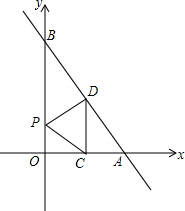 一次函数y=kx+b的图象与x轴、y轴分别交于点A(2,0),B(0,4),O为坐标原点,线段OA、AB的中点分别为点C、D,P为直线OB上一动点.
一次函数y=kx+b的图象与x轴、y轴分别交于点A(2,0),B(0,4),O为坐标原点,线段OA、AB的中点分别为点C、D,P为直线OB上一动点. 如图,AC和BD相交于点O,OA=OC,OB=OD,DC与AB平行吗?为什么?
如图,AC和BD相交于点O,OA=OC,OB=OD,DC与AB平行吗?为什么?