题目内容
9.阅读资料:我们把顶点在圆上,并且一边和圆相交、另一边和圆相切的角叫做弦切角,如图1∠ABC所示.同学们研究发现:P为圆上任意一点,当弦AC经过圆心O时,且AB切⊙O于点A,此时弦切角∠CAB=∠P(图2)证明:∵AB切⊙O于点A,∴∠CAB=90°,又∵AC是直径,∴∠P=90°∴∠CAB=∠P
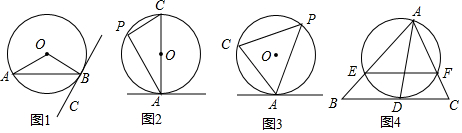
问题拓展:若AC不经过圆心O(如图3),该结论:弦切角∠CAB=∠P还成立吗?请说明理由.
知识运用:如图4,AD是△ABC中∠BAC的平分线,经过点A的⊙O与BC切于点D,与AB、AC分别相交于E、F.求证:EF∥BC.
分析 问题拓展:首先连接AO并延长交⊙O于点D,连接CD,由圆周角定理可得∠D=∠P,又由AD是直径,AB切圆于点A,易证得∠CAB=∠CAD,继而证得结论;
知识运用:连接DF,AD是△ABC中∠BAC的平分线,⊙O与BC切于点D,可得∠FDC=∠EAD,又由圆周角定理可得∠EAD=∠EFD,继而证得结论.
解答  解:问题拓展:成立.
解:问题拓展:成立.
如图3,连接AO并延长交⊙O于点D,连接CD,
则∠D=∠P,
∵AD是直径,
∴∠D+∠CAD=90°,
又∵AB切圆于点A,
∴∠CAB+∠CAD=90°,
∴∠CAB=∠CAD,
而∠CAD=∠P,
∴∠CAB=∠P;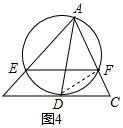 知识运用:如图4,连接DF,
知识运用:如图4,连接DF,
∵AD是△ABC中∠BAC的平分线,
∴∠EAD=∠DAC,
∵⊙O与BC切于点D,
∴∠FDC=∠DAC,
∴∠FDC=∠EAD,
∵在⊙O中∠EAD=∠EFD,
∴∠FDC=∠EFD,
∴EF∥BC.
点评 此题考查了切线的性质、圆周角定理以及平行线的判定.注意准确作出辅助线是解此题的关键.

练习册系列答案
相关题目
19.在-2、0、π、|-5|中最小的数是( )
| A. | -2 | B. | 0 | C. | π | D. | |-5| |
20.某养殖户的养殖成本逐年增长,第一年的养殖成本为12万元,第3年的养殖成本为16万元.设养殖成本平均每年增长的百分率为x,则下面所列方程中正确的是( )
| A. | 12(1-x)2=16 | B. | 16(1-x)2=12 | C. | 16(1+x)2=12 | D. | 12(1+x)2=16 |
4. a,b两数在数轴上的位置如图所示,下列结论中正确的是( )
a,b两数在数轴上的位置如图所示,下列结论中正确的是( )
 a,b两数在数轴上的位置如图所示,下列结论中正确的是( )
a,b两数在数轴上的位置如图所示,下列结论中正确的是( )| A. | a>0,b<0 | B. | a<0,b>0 | C. | ab>0 | D. | 以上均不对 |
1.下列代数式的书写规范的是( )
| A. | m×n | B. | 7ab÷6 | C. | 2$\frac{1}{3}$x | D. | a2-$\frac{1}{a}$ |

 如图,四个有理数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+q=0,则m,n,p,q四个有理数中,绝对值最小的一个是( )
如图,四个有理数m,n,p,q在数轴上对应的点分别为M,N,P,Q,若n+q=0,则m,n,p,q四个有理数中,绝对值最小的一个是( )