题目内容
18.二次函数y=x2-6x+4化成顶点式为y=(x-3)2-5,对称轴是x=3.分析 利用配方法把二次函数y=x2-6x+4从一般式转化为顶点式,直接利用顶点式的特点求解.
解答 解:∵y=x2-6x+4=(x-3)2-5.
∴y=(x-3)2-5,对称轴是x=3.
故答案是:y=(x-3)2-5;x=3.
点评 此题考查二次函数的解析式有三种形式:(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);(2)顶点式:y=a(x-h)2+k;(3)交点式(与x轴):y=a(x-x1)(x-x2).

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
8.一个多边形的每个内角均为150°,则这个多边形是( )
| A. | 九边形 | B. | 十边形 | C. | 十二边形 | D. | 十五边形 |
13.下列方程中,是一元二次方程的是( )
| A. | x2+$\frac{1}{{x}^{2}}$=0 | B. | ax2+bx+c=0 | C. | (x-1)(x-2)=1 | D. | 3x2-2xy-5y2=0 |
10.下列命题中是假命题的是( )
| A. | 同位角相等 | |
| B. | 在同一平面内,垂直于同一直线的两条直线互相平行 | |
| C. | 两角及其中一角的平分线对应相等的两个三角形全等 | |
| D. | 在三角形中,如果一边上的中线等于这一边的一半,那么这条边所对的角是直角 |
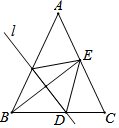 如图,在△ABC中,AB=AC=12$\sqrt{5}$,BC=24,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为13.
如图,在△ABC中,AB=AC=12$\sqrt{5}$,BC=24,如果将△ABC沿直线l翻折后,点B落在边AC的中点E处,直线l与边BC交于点D,那么BD的长为13.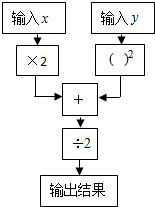 如图是一个数值转换机的示意图.
如图是一个数值转换机的示意图.